25
WORD PROBLEMS
THAT LEAD TO
EQUATIONS WITH FRACTIONS
HERE ARE SOME WORD PROBLEMS that lead to equations with fractions.
Example 1. The whole is equal to the sum of the parts.
This problem is from a classical Hindu text on algebra from the 9th century.
During an amorous struggle, the lady's pearls broke. Half of the pearls fell onto the floor; a fourth rolled under a chair; a sixth fell into her lap; and three pearls remained on the strand. How many were there originally on the strand?
Solution. Let x be that total number. And let us account for them all.
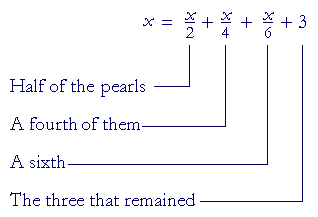
First, we will clear the equation of fractions. The LCM of 2, 4, and 6 is 12. We will multiply every term by 12, and cancel the denominators:
| x | = | x 2 |
+ | x 4 |
+ | x 6 |
+ 3 |
| 12x | = | 6x + 3x + 2x + 36 | |||||
| 12x | = | 11x + 36 | |||||
| 12x − 11x | = | 36 | |||||
| x | = | 36 | |||||
There were originally 36 pearls on the strand.
Example 2. One number is three times another. The sum of their reciprocals is 4. What are the two numbers?
Solution. Let x be the first number. Then the other is three times that: 3x. The problem states that the sum of their reciprocals is 4:
| 1 x |
+ | 1 3x |
= | 4 | |
| Clear of fractions. The LCM is 3x: | |||||
| 3 + 1 | = | 3x· 4 | |||
| That is, | |||||
| 12x | = | 4 | |||
| x | = | 4 12 |
|||
| = | 1 3 |
||||
| 1 3 |
is the first number. The other number is 3· | 1 3 |
= 1. |
(Note that the sum of their reciprocals -- 3 + 1 -- does equal 4.)
Problem 1. Melissa went shopping and spent half of her money on shoes, a third on a blouse, a tenth to take her boyfriend to lunch, and she came home with $12. How much did she start out with?
[Hint: The whole is the sum of the parts.]
Let x = How much she started out with.
Here is the equation:
| x | = |
x 2 |
+ |
x 3 |
+ |
x 10 |
+ 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The LCM is 30. Here is the cleared equation and its solution: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30x | = | 15x + 10x + 3x + 360 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30x − 28x | = | 360 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2x | = | 360 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| x | = | 180 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Problem 2. Half of a number added to its third part, is eight less than the number. What is the number?
To see the equation, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
But do the problem yourself first!
In every case, let x represent the unknown number.
The equation is:
|
x 2 |
+ |
x 3 |
= | x − 8 | |
| The LCM is 6. Here is the cleared equation and its solution: | |||||
| 3x + 2x | = | 6x − 48 | |||
| 5x − 6x | = | −48 | |||
| −x | = | −48 | |||
| x | = | 48 | |||
Problem 3. One number is four times another. The sum of their
| reciprocals is | 5 12 |
. What are the two numbers? |
Let x be the first number. Then the other is 4x. Here is the equation:
|
1 x |
+ |
1 4x |
= |
5 12 |
|
| The LCM is 12x. Here is the cleared equation and its solution: | |||||
| 12 + 3 | = | 5x | |||
| 5x | = | 15 | |||
| x | = | 3. | |||
| 4x | = | 12. | |||
These are the two numbers.
Problem 4. If the same number is added to the numerator and
| denominator of | 7 9 |
the result is | 5 6 |
. What is that number? |
Here is the equation:
|
7 + x 9 + x |
= | 5 6 |
||
| On cross multiplying, here is the cleared equation and its solution: | ||||
| (7 + x)6 | = | (9 + x)5 | ||
| 42 + 6x | = | 45 + 5x | ||
| 6x − 5x | = | 45 − 42 | ||
| x | = | 3 | ||
Time going, time returning problem
Next Lesson: Radicals - Rational and irrational numbers
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
