skill

S k i l l
 i n
A R I T H M E T I C

Table of Contents | Home | Introduction

Lesson 25

ADDING AND SUBTRACTING
FRACTIONS AND MIXED NUMBERS


In this Lesson, we will answer the following:

  1. How do we add or subtract fractions?
  2. How do we add fractions with different denominators?
  3. What number should we choose as the common denominator?
  4. How do we add mixed numbers?

    Section 2

    Subtracting mixed numbers.

A FRACTION IS A NUMBER we need for measuring (Lesson 20); therefore we sometimes have to add or subtract them. Now, to add or subtract anything, the names -- the units -- must be the same.

2 apples + 3 apples = 5 apples.

We cannot add 2 apples plus 3 oranges -- at least not until we call them "pieces of fruit."

In the name of a fraction -- "2 ninths," for example -- ninths is the name of what we are adding.

2 ninths + 3 ninths = 5 ninths.

Lesson 21, Example 3.

That unit will appear as the denominator.
 1.   How do we add or subtract fractions?
 
add fractions
 
  The names of what we are adding or subtracting -- the denominators -- must be the same.  Add or subtract only the numerators, and keep that same denominator.
 

  Example 1.    5
8		  +  2
8		  =  7
8		 .

"5 eighths + 2 eighths = 7 eighths."

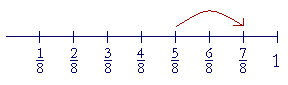
add fractions

The denominator of a fraction has but one function, which is to name what we are counting.  In this example, we are counting eighths.

  Example 2.    5
8		  −  2
8		  =  3
8		 .

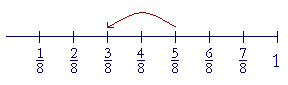
add fractions

Fractions with different denominators

To add or subtract fractions, the denominators must be the same.  Before continuing, then, the student should know how to convert one fraction
to an equivalent one, by multiplying the numerator and the denominator. See Lesson 22, Examples 1, 2, 3, and especially Example 4.
 2.   How do we add fractions with different denominators?
2
3		   +   1
4
 
  Convert each fraction to an equivalent fraction with the same denominator.
 
 3.   What number should we choose as the common denominator?
 
  Choose a common multiple of the original denominators. Choose their lowest common multiple. (Lesson 23.)
 

We choose a common multiple of the denominators because we change a denominator by multiplying it.  Lesson 22.

  Example 3.      2
3		  +  1
4		 .

Solution.  The lowest common multiple of 3 and 4 is their product, 12. (Lesson 22, Question 4.)

We will convert each fraction to an equivalent fraction with denominator 12.

2
3		  +  1
4		  =   8 
12		  +   3 
12
 
       =  11
12		 . 
We converted   2
3		  to   8 
12		   by saying, "3 goes into

(is contained in) 12 four times. Four times 2 is 8."

(In that way, we multiplied both 2 and 3 by the same number, namely 4.  See Lesson 22, Question 3.)

We converted   1
4		  to   3 
12		   by saying, "4 goes into 12 three

times. Three times 1 is 3."  (We multiplied both 1 and 4 by 3.)

The fact that we say what we do shows again that arithmetic is a spoken skill.

In practice, it is necessary to write the common denominator only once:

2
3		  +  1
4		  =  8 + 3
  12		  =  11
12		 .
  Example 4.     4
5		  +   2 
15

Solution.  The LCM of 5 and 15  is 15.  Therefore,

4
5		  +   2 
15		  =  12  +  2
    15		  =  14
15		 .
We changed   4
5		  to  12
15		   by saying, "5 goes into 15 three

times. Three times 4 is 12."

We did not change   2 
15		  , because we are not changing the

denominator 15.


  Example 5.      2
3		  +  1
6		  +   7 
12

Solution.  The LCM of 3, 6, and 12  is 12.


2
3		  +  1
6		  +   7 
12		   =   8 + 2 + 7
     12
2
3		  +  1
6		  +   7 
12		   =   17
12
2
3		  +  1
6		  +   7 
12		   =  1  5 
12		 .
We converted   2
3		   to    8 
12		   by saying, "3 goes into 12 four

times. Four times 2 is 8."

We converted   1
6		   to    2 
12		   by saying, "6 goes into 12 two

times. Two times 1 is 2."

  We did not change   7 
12		  , because we are not changing the

denominator 12.

Finally, we changed the improper fraction   17
12		   to  1  5 
12		   by

dividing 17 by 12. (Lesson 20.)

"12 goes into 17 one (1) time with remainder 5."


  Example 6.     5
6		  +  7
9

Solution.  The LCM of 6 and 9  is 18.


5
6		  +  7
9		   =   15 + 14
   18		   =   29
18		   =  1 11
18		 .
We changed   5
6		   to   15
18		   by multiplying both terms by 3.
We changed   7
9		   to   14
18		   by multiplying both terms by 2.

  Example 7.    Add mentally   1
2		  +  1
4		 .
  Answer.    1
2		  is how many  1
4		 's?
1
2		  =  2
4		 .

Just as 1 is half of 2, so 2 is half of 4.  Therefore,

1
2		  +  1
4		  =  3
4		 .

The student should not have to write any problem in which one of

  the fractions is  1
2		 , and the denominator of the other is even.

For example,

1
2		  +   2 
10		  =   7 
10
  -- because   1
2		  =   5 
10		 .

Example 8.   In a recent exam, one eighth of the students got A, two fifths got B, and the rest got C.  What fraction got C?

 Solution.   Let 1 represent the whole number of students.  Then the question is:

1
8		  +  2
5		  + ?  = 1 .

Now,

1
8		  +  2
5		  =  5 + 16
   40		  =  21
40		 .
The rest, the fraction that got C, is the complement of   21
40		 .
It is  19
40		 .

 4.   How do we add mixed numbers?
add fractions
  Add the whole numbers and add the fractions separately.

  Example 9.    4 3
8		   +  2 2
8		   =  6 5
8		 .

  Example 10.    3 2
5		   +  1 4
5		   =  4 6
5		 .
But  6
5		  is improper, we must change it to a mixed number:
46
  5		  = 1 1
5		 .

Therefore,

4 6
5		   =  4 + 1 1
5		   =  5 1
5		 .

add fractions

Solution.  When the denominators are different, we may arrange the work vertically; although that is not necessary.

To add the fractions, the denominators must be the same.  The LCM

  of 4 and 8  is 8.  We will change  3
4		  to  6
8		 -- by multiplying

both terms by 2:

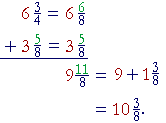
add fractions

  We added  6 + 3 = 9.    6
8		  +  5
8		  =  11
 8 		  = 1 3
8		 .
     9 + 1 3
8		  = 10 3
8		 .

At this point, please "turn" the page and do some Problems.

or

Continue on to Section 2:  Subtracting mixed numbers

Introduction | Home | Table of Contents

Copyright © 2021 Lawrence Spector

Questions or comments?

E-mail:  teacher@themathpage.com