Book I. Propositions 13-14
Problems
1. a) State the hypothesis of Proposition 13.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload")
Do the problem yourself first!
A straight line that stands on another straight line makes two angles.
1. b) State its conclusion.
Either it makes two right angles, or it makes angles that together are equal to two right angles.
1. c) On which prior proposition does Proposition 13 depend?
1. d) Practice Proposition 13.
2. a) State the hypothesis of Proposition 14.
Two straight lines are on opposite sides of a given straight line, and, meeting at one point of that line they make the adjacent angles equal to two right angles.
2. b) State its conclusion.
Those two straight lines are in a straight line with one another.
2. c) Practice Proposition 14.
3. a) State a partial converse of Proposition 14.
If two straight lines are on opposite sides of a given straight line, and are in a straight line with one another, then the adjacent angles that are made are equal to two right angles.
3. b) Prove that partial converse.
It follows from Proposition 13.
4. Prove: All straight angles are equal to one another.
Since all right angles are equal to one another (Postulate 4), then all angles equal to two right angles — a straight angle — will equal other angles equal to two right angles.
5. AB, CD are straight lines that intersect at the point E.
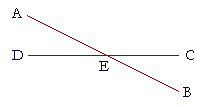
3. a) Name two straight angles.
Angles AEB and DEC.
5. b) Name two angles that are supplements of angle AED.
Angles AEC and DEB.
5. c) Prove that those two angles are equal. That is prove:
Angles that are supplements of the same angle are equal to one another.

[Hint: Axiom 3.]
The straight angle AEB is equal to the straight angle DEC. From each of those equals take away angle AED. Then what remains will be equal: Angle DEB (what remains from AEB) will equal angle AEC (what remains from DEC).
6. ABCD is a straight line, and triangle BEC is isosceles, with EB equal
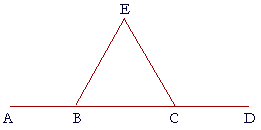
to EC. Prove that angle EBA is equal to angle ECD.
Angles EBA, EBC are equal to two right angles;
and angles ECD, ECB are also equal to two right angles.
But angle ECB is equal to angle EBC
because triangle BEC is isosceles.
Therefore on subtracting those equal angles from those pairs of equals,
angle EBA is equal to angle ECD.
This effectively proves:
Angles that are supplements of equal angles are equal to one another.
Table of Contents | Introduction | Home
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com