Book I. Propositions 9 and 10
Problems
Back to Propositions 9 and 10.
1. Draw an angle, and bisect it.
2. a) In Proposition 9, what are we given?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
An angle.
2. b) What are we required to do?
Bisect it.
2. c) Practice Proposition 9.
3. Use Proposition 9 to prove: In an isosceles triangle the angles at the base are
3. equal.
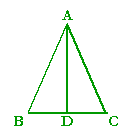
Let ABC be an isosceles triangle with AB equal to AC. Then angle ABC is equal to angle ACB
Bisect angle BAC with the straight line AD.
Then, since BA is equal to CA, and AD is common to the two triangles ADB, ADC,
the two sides BA, AD are equal to the two sides CA, AD respectively;
and we have constructed angle BAD equal to angle CAD.
Therefore triangles BAD, CAD are congruent. (S.A.S.)
And those angles are equal that are opposite the equal sides:
therefore angle ABD is equal to angle ACD.
4. Draw a straight line, and bisect it.
5. a) In Proposition 10, what are we given?
A straight line.
4. b) What are we required to do?
Bisect it.
5. c) Practice Proposition 10.
Table of Contents | Introduction | Home
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com