Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

THE THEORY OF PARALLEL LINES
Book I. Propositions 27 and 28
WE NOW BEGIN the second part of Euclid's First Book. We have accomplished the basic constructions, we have proved the basic relations between the sides and angles of a triangle, and in particular we have found conditions for triangles to be congruent. Euclid now shows when figures that are not congruent will be equal; equal areas that is. And finally we will reach the goal of Book I, which is the celebrated theorem of Pythagoras -- about the equality of the squares drawn on the sides of a right triangle.
The propositions that follow all depend on the theory of parallel lines. We begin with some terminology.
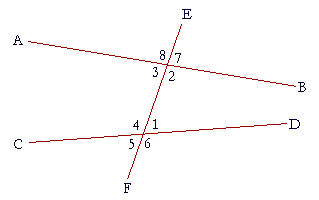
When a straight line meets two other straight lines, as EF meets AB and CD, it forms angles, which we name as follows:
We call angles 1, 2, 3, 4 the interior angles, while angles 5, 6, 7, 8 are the exterior.
Angles 1 and 3 are called alternate angles, as are angles 2 and 4. (For if we start at angle 1 and go around, those angles alternate.)
Angles 8 and 3 are adjacent angles, as are 8 and 7; 1 and 6; and so on.
We relate an exterior to an interior angle as follows: With respect to angle 7, for example, we say that angle 1 is the opposite interior angle on the same side. (With respect to angle 6, on the other hand, angle 1 is the adjacent interior angle on the same side.)
We now begin the theory of parallel lines. It depends, as it must, on the definition. We repeat it here:
Parallel lines are straight lines that are in the same plane and
do not meet, no matter how far extended in either direction.
Now, how could we possibly know whether straight lines will never meet? The following theorem will answer that. It establishes a sufficient condition for lines to be parallel. And since there is no other condition, this one will have to be proved indirectly.
PROPOSITION 27. THEOREM
| If a straight line that meets two straight lines makes the alternate angles equal, then the two straight lines are parallel. | |
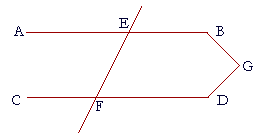
| Let EF be a straight line that meets the two straight lines AB, CD, and let it make the alternate angles AEF, EFD equal. Then AB is parallel to CD. |
|
 |
|
| For if AB is not parallel to CD, then when extended they will meet | |
| either in the direction of B, D or in the direction of A, C. | |
| Let them be extended so that they meet in the direction of B, D at G. | |
| Then EGF is a triangle; | |
| and its exterior angle AEF is greater than the opposite interior angle EFG. | |
| (I. 16) | |
| But angle AEF is also equal to angle EFG; | (Hypothesis) |
| which is impossible. | |
| Therefore AB, CD when extended will not meet in the direction of B, D. | |
| In the same way, we can prove that they will not meet in the direction of A, C. | |
| But straight lines that do not meet, no matter how far extended in either | |
| direction, are parallel. | (Definition. 14) |
| Therefore AB is parallel to CD. | |
| Therefore, if a straight line etc. Q.E.D. | |
![]()
So, the question "How could we possibly know whether straight lines will never meet?" -- that is, whether they are parallel -- is answered by the method of contradiction. With the hypothesis the alternate angles are equal, we assume that the straight lines would meet; Proposition 16 then forces the contradiction.
We now then have a sufficient condition for proving two lines parallel. We need only show that when a straight line meets them, the alternate angles are equal.
Proposition 28 follows directly from Proposition 27, and it gives another condition for recognizing parallel lines; actually, two conditions.
PROPOSITION 28. THEOREM
| If a straight line that meets two straight lines makes an exterior angle equal to the opposite interior angle on the same side, or if it makes the interior angles on the same side equal to two right angles, then the two straight lines are parallel. | |
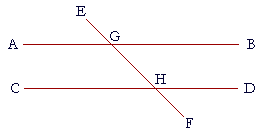
| Let the straight line EF meet the two straight lines AB, CD, and let it make the exterior angle EGB equal to the opposite interior angle GHD, or let it make the interior angles on the same side, angles BGH, GHD together, equal to two right angles; then AB will be parallel to CD. |
|
 |
|
| For, since angle EGB is equal to angle GHD, | (Hypothesis) |
| and angle AGH is also equal to angle EGB; | (I. 15) |
| then angle AGH is equal to angle GHD; | (Axiom 1) |
| and they are alternate angles; | |
| therefore AB is parallel to CD. | (I. 27) |
| Next, since angles BGH, GHD are together equal to two right angles, | (Hypothesis) |
| and angles AGH, BGH are also equal to two right angles, | (I. 13) |
| then angles AGH, BGH are equal to angles BGH, GHD. | |
| Take away the common angle BGH; | |
| therefore the remaining angle AGH is equal to the remaining angle GHD; | (Axiom 3) |
| and they are alternate angles; | |
| therefore AB is parallel to CD. | (I. 27) |
| Therefore, if a straight line etc. Q.E.D. | |
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com