Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

CONGRUENCE
Side-angle-side: SAS
Book I. Proposition 4
HERE AGAIN is Axiom 4:
Things that coincide with one another
are equal to one another.
This means that if we have two triangles, ABC, DEF, say, and if we
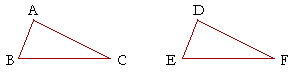
could place them one on the other; and if AB were to coincide with DE, and BC with EF, and CA with FD, then we could conclude that those triangles were equal to one another in all respects. Their respective angles would be equal, and the triangles themselves would be equal areas. When figures would coincide in that way, we say that they are congruent.
Axiom 4 therefore states a sufficient condition for equality, namely congruence. That is obvious; that is why it is an axiom.
If we can show, then, that two triangles are congruent, we will know the following:
1) Their corresponding sides are equal.
2) Their corresponding angles are equal.
3) They are equal areas.
Those are the three magnitudes of plane geometry: length (the sides), angle, and area. Congruence is our first way of knowing that magnitudes of the same kind are equal.
What are sufficient conditions, then, for triangles to be congruent?
Side-angle-side

The fundamental condition for congruence is that two sides and the included angle of one triangle be equal to two sides and the included angle of the other.
Euclid proved this by supposing one triangle actually placed on the other, and allowing the equal sides and equal angles to coincide. He then argued that the remaining sides must also coincide. (You might perform this mental experiment yourself.) This is called proof by superposition. And it is out of favor these days. It was even called into question in Euclid's time -- why not prove every theorem by superposition?
If superposition, then, is the only way to see the truth of a proposition, then that proposition ranks with our basic understanding; it is a kind of mental, experimental result. Therefore it should be a first principle, not a theorem.
Nowadays, this proposition is accepted as a postulate. We shall not prove it either.
PROPOSITION 4
If two triangles have two sides equal to two sides respectively, and if the angles contained by those sides are also equal, then the remaining side will equal the remaining side, the triangles themselves will be equal areas, and the remaining angles will be equal, namely those that are opposite the equal sides.
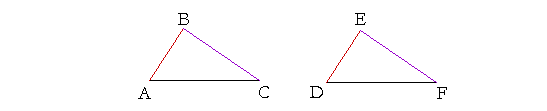
Let triangles ABC, DEF have the two sides AB, BC equal to the two sides DE, EF respectively;
and let the angle at B equal the angle at E;
then the remaining side AC will equal the remaining side DF,
the triangles themselves will be equal areas,
and angle A, opposite side BC, will equal angle D, opposite the equal side EF,
and angle C, opposite side AB, will equal angle F, opposite the equal side DE.
![]()
The expression equal "respectively" means each one to each one. It is in distinction to "together" equal, which would mean that the AB, BC when added would equal DE, EF when added.
It is common to refer to this proposition as "S. A. S.": Side-Angle-Side. When that condition is satisfied, the two triangles will be equal in all respects.
Here are examples of how we use S.A.S. to prove equality.
Example 1. Let ABC, CDE be triangles with AC equal to CE,
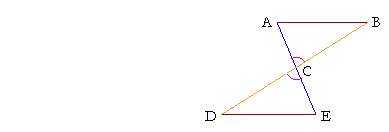
DC equal to CB, and angle ACB equal to angle DCE.
Which other angles are equal?
Solution. Even though we may see that the triangles are congruent (S.A.S.), it may not be immediately clear which are the equal angles. They are those that are opposite the equal sides:
Angle A, opposite side BC, is equal to angle E, opposite the equal side DC;
and angle B, opposite side AC, is equal to angle D, opposite the equal side CE.
Example 2. In this figure, AB is equal to AC, and AE is equal to AD. Prove that BE is equal to DC.
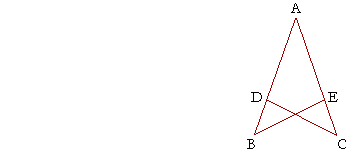
Solution. The student should see the overlapping triangles ABE, ACD. Then, since AB is equal to AC, and AE to AD,
the two sides AB, AE (of triangle ABE) are equal to the two sides AC, AD (of triangle ACD) respectively;
and those sides contain a common angle, angle BAC;
therefore -- S.A.S. -- the remaining side of triangle ABE is equal to the remaining side of triangle ACD: BE is equal to DC.
Which is what we wanted to prove.
![]()
We see, then, that the elementary way to show that lines or angles are equal, is to show that they are corresponding parts of congruent triangles. The sufficient condition here for congruence is side-angle-side. We will see that other conditions are side-side-side, Proposition 8, and angle-side-angle, Proposition 26. There is also the so-called ambiguous case, side-side-angle. It will be possible to prove a special instance of that case when have proved the Pythagorean theorem; it will be Problem 4 of that topic.
As we continue, however, we will see that congruence -- coinciding -- is just one condition for equality. For, isn't it possible that a straight line might be equal in length to a curved line? And aren't there two squares that together might have the same area as one square? We will want to extend our knowledge of figures beyond simple congruence. The issue will be equality itself.
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com