Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

BISECTIONS
Book I. Propositions 9 and 10
WE WILL NOW solve the problem of bisecting an angle, that is, dividing it into two equal angles, and of bisecting a straight line.
Bisecting an angle
Here is how to bisect the angle BAC:
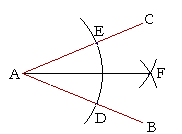
Place the point of the compass on A, and swing an arc ED.
Then, with D as center and DE as radius, draw an arc.
Keeping the same radius and with E as center, draw an arc that will intersect the first; call that point of intersection F, and draw AF.
Then AF bisects angle BAC.
For, if we were to complete the equilateral triangle DEF, then triangles AEF, ADF would be congruent. This is the following proposition.
PROPOSITION 9. PROBLEM
| To bisect a given angle. | |
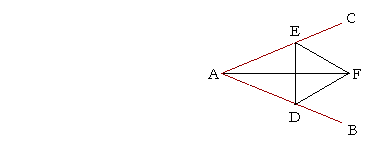
| Let angle BAC be the given angle; we are required to bisect it. | |
 |
|
| Choose any point D on AB; | |
| from AC cut off AE equal to AD; | (I. 3) |
| draw DE, and on it construct the equilateral triangle DEF; | (I. 1) |
| and join AF. | |
| Then we have bisected angle BAC by the straight line AF. | |
| For, since AE is equal to AD, | (Construction) |
| and AF is common to triangles EAF, DAF, | |
| the two sides EA, AF are equal to the two sides DA, AF respectively. | |
| And the base EF is equal to the base DF; | (Construction) |
| therefore angle DAF is equal to angle EAF. | (S.S.S.) |
| Therefore we have bisected the given angle BAC by the straight line AF. Q.E.F. | |
![]()
So much for bisecting any angle. One of the "problems of antiquity" was to trisect any angle. Scholars, both professional and amateur, learned much about geometry as they struggled with the task for more than 2000 years, and some still do. It was not until the 19th century that it was proved that the trisection of any angle, using straightedge and compass, is impossible.
In the proof of Proposition 9, note that the side EF is called the base, as is the side DF. Why? Because Proposition 8 -- S.S.S. -- which allows us to conclude that those angles are equal, enunciates that the bases are also equal. By quoting the exact words of a previous proposition in that way, in a virtually legalistic manner, we make the sequence of reasoning perfectly clear.
To bisect a straight line
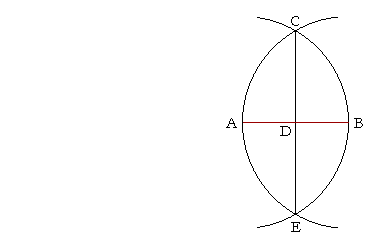
To bisect the straight line AB, place the point of the compass at A, and with radius AB draw an arc. Now place the point of the compass at B, and with the same radius draw an arc. Upon connecting their points of intersection C and E, the line CE cuts AB into two equal parts at D.
The student should attempt the proof before reading it below.
PROPOSITION 10. PROBLEM
| To bisect a given straight line. | |
| Let AB be the given straight line; we are required to cut it into two equal parts. | |
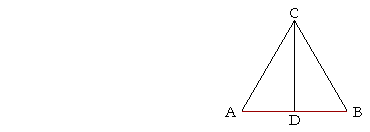 |
|
| On AB draw the equilateral triangle ABC, | (I. 1) |
| and bisect angle ACB by the straight line CD, meeting AB at D. | (I. 9) |
| Then AB will be cut into two equal parts at the point D. | |
| For, since AC is equal to CB, | (Definition 9) |
| and CD is common to triangles ACD, BCD, | |
| then the two sides AC, CD are equal to the two sides BC, CD respectively; | |
| and angle ACD is equal to angle BCD; | (Construction) |
| therefore the remaining side AD is equal to the remaining side DB. | |
| (S.A.S.) | |
| Therefore we have cut the given straight line AB into two equal parts at the point D. Q.E.F. | |
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com