7
THE CHAIN RULE
The derivative of a function of a function
The derivative of a function of a function
f (x) = x5 and g(x) = x2+ 1.
If we now let g(x) be the argument of f, then f will be a function of g.
f (g(x)) = (x2+ 1)5.
What is the derivative of f (g(x)) ?
First, note that
| d f(x) dx |
= 5x4. |
That is: The derivative of f with respect to its argument (which in this case is x) is equal to 5 times the 4th power of the argument.
This means that if g -- or any variable -- is the argument of f, the same form applies:
| d f(g) dg |
= 5g4. |
| d f(h) dh |
= 5h4. |
| d f(v) dv |
= 5v4. |
In other words, we can really take the derivative of a function of an argument only with respect to that argument.
Therefore, since g = x2+ 1,
| d f(g) dg |
= 5g4 | = 5(x2+ 1)4. |
Next, the derivative of g is 2x. What is called the chain rule states the following:
| df(g(x)) dx |
= | df(g) dg |
· | dg(x) dx |
"If f is a function of g and g is a function of x,
then the derivative of f with respect to x
is equal to the derivative of f(g) with respect to g
times the derivative of g(x) with respect to x."
Therefore according to the chain rule, the derivative of
(x2+ 1)5
is
5(x2+ 1)4· 2x.
Note: In (x2+ 1)5, x2+ 1 is "inside" the 5th power, which is "outside." We take the derivative from outside to inside. When we take the outside derivative, we do not change what is inside. We then multiply by the derivative of what is inside.
To decide which function is outside, decide which you would have to evaluate last.
To evaluate
(x2+ 1)5,
you would first have to evaluate x2+ 1. Then you would take its 5th power. The 5th power therefore is outside. That is why we take that derivative first.
When we write f(g(x)), f is outside g. We take the derivative of f with respect to g first.
| Example 1. f(x) = |
Solution. This has the form f (g(x)). What function is f, that is, what is outside, and what is g, which is inside?
g is x4 − 2 because that is inside the square root function, which is f. The derivative of the square root is given in the Example of Lesson 6. For any argument g of the square root function,
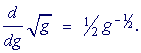
Here, g is x4 − 2. Therefore, since the derivative of x4 − 2 is 4x3,
| d dx |
= ½(x4 − 2)−½· 4x3 = 2x3(x4 − 2)−½. |
Example 2. What is the derivative of y = sin3x ?
Solution. This is the 3rd power of sin x. To decide which function is outside, how would you evaluate that?
You would first evaluate sin x, and then take its 3rd power. sin x is inside the 3rd power, which is outside.
Now, the derivative of the 3rd power -- of g3 -- is 3g2. Therefore, accepting for the moment that the derivative of sin x is cos x (Lesson 12), the derivative of sin3x -- from outside to inside -- is
3 sin2x· cos x.
| Example 3. What is the derivative of | 1 x3 + 1 |
? |
| Solution. x3 + 1 is inside the function | 1 x |
= x−1, |
whose derivative is −x−2 ; (Problem 4, Lesson 4). We have, then,
| 1 x3 + 1 |
= | (x3 + 1)−1 | . |
Therefore, its derivative is
−(x3 + 1)−2· 3x2
Example 4. Assume that y is a function of x. y = y(x). Apply the chain rule to
| d dx |
y2 | . |
| Solution. | dy2 dx |
= | dy2 dy |
· | dy dx |
= | 2y | dy dx |
. |
y, which we are assuming to be a function of x, is inside the function y2. The derivative of y2with respect to y is 2y. As for the derivative of
| y with respect to x, we indicate it as | dy dx |
. (See Lesson 5.) |
Problem 1. Calculate the derivative of (x2−3x + 5)9.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
9(x2−3x + 5)8(2x − 3)
Problem 2. Calculate the derivative of (x4 − 3x2+ 4)2/3.
2/3(x4 − 3x2+ 4)−1/3(4x3 − 6x)
Problem 3. Calculate the derivative of sin5x.
5 sin4x cos x
Problem 4. Calculate the derivative of sin x5.
The inside function is x5 -- you would evaluate that last. The outside function is sin x. (This is the sine of x5.) Therefore, the derivative is
cos x5· 5x4.
Problem 5. Calculate the derivative of sin (1 + 2![]() ).
).
cos (1 + 2![]() )x−1/2.
)x−1/2.
Problem 6. Calculate the derivative of ![]()
¼(sin x)−3/4 cos x.
Example 5. More than two functions. The chain rule can be extended to more than two functions. For example, let
| f(x) | = | . |
The outside function is the square root. Inside that is (1 + a 2nd power). And inside that is sin x.
The derivative therefore is
| ½(1 + sin2x)−1/2· 2 sin x· cos x | = | sin x cos x |
. |
| Problem 7. Calculate the derivative of | 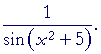 |
(Compare Example 3.)
| −[sin (x2+ 5)]−2· cos (x2+ 5)· 2x | = | − |
2x cos (x2+ 5) sin2(x2+ 5) |
| Problem 8. Calculate the derivative of |
Problem 9. Assume that y is a function of x, and apply the chain rule to express each derivative with respect to x.
| a) | d dx |
y3 = | 3y2 | dy dx |
| b) | d dx |
sin y = | cos y | dy dx |
| c) | d dx |
½y−½ | dy dx |
Proof of the chain rule
To prove the chain rule let us go back to basics. Let f be a function of g, which in turn is a function of x, so that we have f(g(x)). Then when the value of g changes by an amount Δg, the value of f will change by an amount Δf. We will have the ratio
| Δf Δg |
. |
Again, since g is a function of x, then when x changes by an amount Δx, g will change by an amount Δg. We will have the ratio
| Δg Δx |
. |
But the change in x affects f because it depends on g. We will have
| Δf Δx |
. It will be the product of those ratios: |
| Δf Δx |
= | Δf Δg |
· | Δg Δx |
. |
Let us now take the limit as Δx approaches 0. Then the change in g(x) -- Δg -- will also approach 0. Therefore, since the limit of a product is equal to the product of the limits (Lesson 2), and by definition of the derivative:
| df dx |
= | df dg |
· | dg dx |
This is the chain rule.
![]()
Next Lesson: The quotient rule
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
