16
SYMMETRY
Test for symmetry: Even and odd functions
LET THIS BE THE RIGHT-HAND SIDE of the graph of a function:
We will now draw the left-hand side -- so that the graph will be symmetrical with respect to the y-axis:
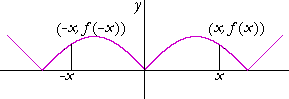
In this case,
f(−x) = f(x).
The height of the curve at −x is equal to the height of the curve at x -- for every x in the domain of f.
Again, let this be the right-hand side:

We will now draw the left-hand side -- so that the graph will be symmetrical with respect to the origin:
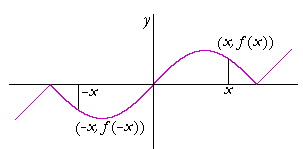
Every point on the right-hand side is reflected through the origin. In this case,
f(−x) = −f(x).
The value of f at −x is the negative of the value at x.
(A reflection through the origin is equivalent to a reflection about the y-axis, followed by a reflection about the x-axis.)
Test for symmetry: Even and odd functions
Symmetry, then, depends on the behavior of f(x) on the other side of the y-axis -- at minus-x : f(−x).
Here is the test:
If f(−x) = f(x),
then the graph of f(x) is symmetrical with respect to the y-axis.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
If f(−x) = −f(x),
then the graph of f(x) is symmetrical with respect to the origin.
A function symmetrical with respect to the y-axis is called an even function.
A function that is symmetrical with respect to the origin is called an odd function.
Example 1. Test this function for symmetry:
f(x) = x4 + x2 + 3
Solution. We must look at f(−x):
| f(−x) | = | (−x)4 + (−x)2 + 3 |
| = | x4 + x2 + 3 | |
| = | f(x). | |
Since f(−x) = f(x), this function is symmetrical with respect to the y-axis. It is an even function.
Example 2. Test this function for symmetry:
f(x) = x5 + x3 + x
Solution. Again, we must look at f(−x):
| f(−x) | = | (−x)5 + (−x)3 + (−x) |
| = | −x5 − x3 − x | |
| = | −(x5 + x3 + x) | |
| = | −f(x). | |
Since f(−x) = −f(x), this function is symmetrical with respect to the origin. It is an odd function.
Problem. Test each of the following for symmetry. Is f(x) even, odd, or neither?
a) f(x) = x3 + x2 + x + 1
Answer. Neither, because f(−x) ≠ f(x) , and f(−x) ≠ −f(x).
b) f(x) = 2x3 − 4x
Answer. f(x) is odd—it is symmetrical with respect to the origin—because f(−x) = −f(x).
c) f(x) = 7x2 − 11
Answer. f(x) is even—it is symmetrical with respect to the y-axis—because f(−x) = f(x).
Note: A polynomial will be an even function when all the exponents are even.
A polynomial will be an odd function when all the exponents are odd.
But there are even and odd functions that are not polynomials. In trigonometry, y = cos x is an even function, while y = sin x is odd.
Therefore, the issue is the test of f(−x).
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
