 |  |
17
TRANSLATIONS
Vertical stretches and shrinks
A TRANSLATION OF A GRAPH is its rigid movement, vertically or horizontally.
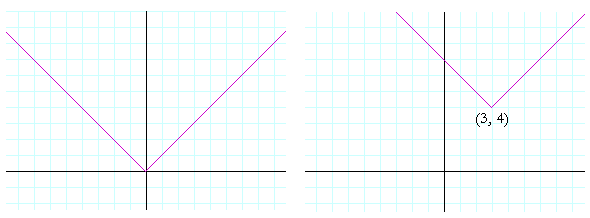
On the left is the graph of the absolute value function. On the right is its translation to a "new origin" at (3, 4).
The equation of the absolute value function is
y = |x|.
The equation of its translation to (3, 4) is
y − 4 = |x − 3|.
For, when x = 3, then y − 4 = 0, that is, y = 4.
Thus the point (3, 4) is that point on the translated graph that was originally at (0, 0).
In general,
| If the graph of | ||||
| y | = | f(x) | ||
| is translated a units horizontally and b units | ||||
| vertically, then the equation of the translated | ||||
| graph is | ||||
| y − b | = | f(x − a). | ||
When f(x) is translated a units horizontally, then the argument of f(x) becomes x − a. In the example above, the argument of |x| becomes x − 3.
We will prove that below.
Example 1. Write the equation of this graph:
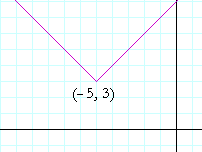
Answer. y − 3 = |x + 5|.
The graph of the absolute value has been translated 3 units up, but 5 units to the left. a = −5. Therefore, x − a becomes
x − (−5) = x + 5.
Problem 1. Write the equation of this graph:
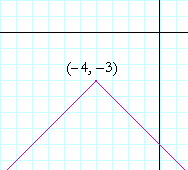
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
y + 3 = −|x + 4|.
Not only has the graph of the absolute value been translated, it has first been reflected about the x-axis.
A translation is a rigid movement of the graph. The reflected graph is the rigid movement of y = −|x|. The reflection therefore takes place before the translation to x = −4. In other words, if you wrote the unreflected translation to (−3, −4) as
y = |x + 4| − 3,
and then wrote the relection about the x-axis as
y = −|x + 4| + 3,
that would be wrong. You could see that because when x = −4, y does not equal −3.
Problem 2. Sketch the graph of y = |x − 3|.
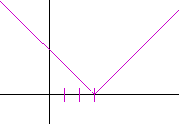
Problem 3. Sketch the graph of y = −|x + 2|.
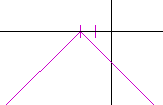
Problem 4. Sketch the graph of y = −|x − 3| + 2.
This is equivalent to y − 2 = −|x − 3|.
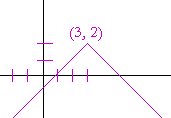
The graph is reflected about the x-axis, and translated to (3, 2).
Problem 5. Sketch the graph of y = 
.
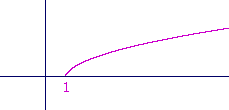
This is the square root function translated 1 unit to the right.
Problem 6. Sketch the graph of y = −
.
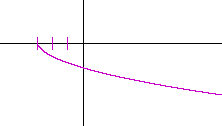
This is the reflected square root function, translated 3 units to the left.
Problem 7. Sketch the graph of y = 1 − x².
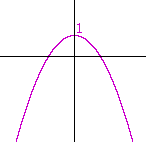
This is equivalent to y − 1 = −x², which is the reflected parabola translated 1 unit up.
Example 2. The vertex of a parabola. Write the equation of the parabola (with leading coefficient 1) whose vertex is at the point (a, b).
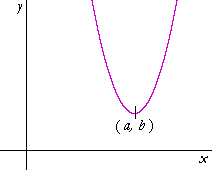
Answer. y − b = (x − a)². This is a translation of y = x² to (a, b).
Problem 8. Write the equation of the parabola whose vertex is at
| a) (1, 2) | y − 2 = (x − 1)² |
| b) (−1, 2) | y − 2 = (x + 1)² |
| c) (1, −2) | y + 2 = (x − 1)² |
Example 3. What are the coördinates of the vertex of this parabola?
| y | = | x² + 6x + 9 |
| Solution. To answer, we must make the equation look like this -- | ||
| y − b | = | (x − a)² |
The vertex will then be at (a, b).
Now, x² + 6x + 9 is the perfect square of (x + 3):
y = x² + 6x + 9 = (x + 3)².
Therefore, a = −3, and b = 0. The vertex is at (−3, 0.)
Example 4. What are the coördinates of the vertex of this parabola?
y = x² + 5
Solution. Again, we must make the equation look like this:
y − b = (x − a)².
If we simply transpose 5 --
y − 5 = x²
-- we see that a = 0, and b = 5. The vertex is at (0, 5).
Example 5. Completing the square. What are the coördinates of the vertex of this parabola?
| y | = | x² + 6x −2 |
| Solution. To make this form -- | ||
| y − b | = | (x − a)² |
-- we will transpose the constant term, and complete the square on the right.
| y + 2 | = | x² + 6x |
| Complete the square by adding 9 to both sides: | ||
| y + 2 + 9 | = | x² + 6x + 9 |
| y + 11 | = | (x + 3)² |
The vertex is at (−3, −11).
Problem 9. What are the coördinates of the vertex of this parabola?
y = x² − 10x + 25
The right-hand side is the perfect square of (x − 5).
y = (x − 5)²
The vertex therefore is at (5, 0).
Problem 10. What are the coördinates of the vertex of this parabola?
y = x² − 1
The equation implies
y + 1 = x².
The vertex is at (0 −1).
Problem 11. What are the coördinates of the vertex of this parabola?
y = x² − 8x + 1
Transpose the constant term, and complete the square on the right:
| y − 1 | = | x² − 8x |
| y − 1 + 16 | = | x² − 8x + 16 |
| y + 15 | = | (x − 4)² |
The vertex is at (4, −15).
The equation of a circle
What characterizes every point (x, y) on the circumference of a circle?
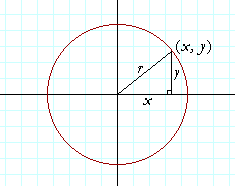
Every point (x, y) is the same distance r from the center. Therefore, according to the Pythagorean distance formula for the distance of a point from the origin:
x² + y² = r².
This is the equation of a circle of radius r, with center at the origin (0, 0).
Specifically, this --
x² + y² = 25
-- is the equation of a circle of radius 5 centered at the origin.
Every pair of values (x, y) that solves that equation, that is, that makes it a true statement, will be the coördinates of a point on the circumference.
Question. What is the equation of a circle with center at (a, b) and radius r?
Answer. (x − a)² + (y − b)² = r².
The circle has been translated from (0, 0) to (a, b).
Problem 12. Write the equation of the circle of radius 3, and center at the following point.
| a) (1, 2) | (x − 1)² + (y − 2)² = 9 |
| b) (−1, −2) | (x + 1)² + (y + 2)² = 9 |
| c) (1, −2) | (x − 1)² + (y + 2)² = 9 |
Example 6. Show that the following is the equation of a circle. Name the radius and the coördinates of the center.
x² − 4x + y² − 2y = 11
Solution. To show that something is the equation of a circle, we must show that it can have this form,
(x − a)² + (y − b)² = r².
Therefore, we will complete the square in both x and y.
To complete the square in x, we will add 4 to both sides.
To complete the square in y, we will add 1 to both sides.
| (x² − 4x + 4) + (y² − 2y + 1) | = | 11 + 4 + 1 |
| (x − 2)² + (y − 1)² | = | 16. |
This is the equation of a circle of radius 4, whose center is at (2, 1).
We can say then that when a quadratic in x plus a quadratic in y is equal to a number --
x² − 4x + y² − 2y = 11
-- then that is the equation of a circle.
The coefficients of x² and y² are 1. And the number must be greater than the negative of the sum of the squares of half the coefficients of x and y.
Problem 13. Show that the following is the equation of a circle. Name the radius and the coördinates of the center.
x² + 6x + y² + 10y − 2 = 0
Transpose the constant term, and complete the square in both x and y. Add the same square numbers to both sides:
| (x² + 6x + 9) + (y² + 10y + 25) | = | 2 + 9 + 25 |
| (x + 3)² + (y + 5)² | = | 36 |
This is the equation of a circle of radius 6, with center at (−3, −5).
Here is the proof of the main theorem.
Theorem. If the graph of y = f (x) is translated a units horizontally and b units vertically, then the equation of the translated graph is
y − b = f(x − a).
For in a translation, every point on the graph moves in the same manner. Let (x1, y1), then, be the coördinates of any point on the graph of y = f (x), so that
y1 = f (x1).
And let us translate the graph a units horizontally and b units vertically, so that x1 goes to the point
x1 + a,
and y1 goes to the point
y1 + b.
If a is a positive number, then that point will be to the right of x1, while if a is negative, it will be to the left. Similarly, if b is a positive number, then y1 + b will be above y1, while if b is negative, it will be below.
Now, what will be the equation of the translated graph, such that when the value of x in the equation is x1 + a, the value of y will be y1 + b?
We say that the following is the equation:
y − b = f(x − a).
For, when x = x1 + a:
y − b = f(x1 + a − a) = f(x1) = y1;
y = y1 + b.
And (x1, y1) is any point on the graph of y = f (x). Therefore the equation of the translated graph is
y − b = f(x − a).
Which is what we wanted to prove.
Vertical stretches and shrinks
If we multiply a function f(x) by a number c -- producing c f(x) -- what will be the effect on the graph?
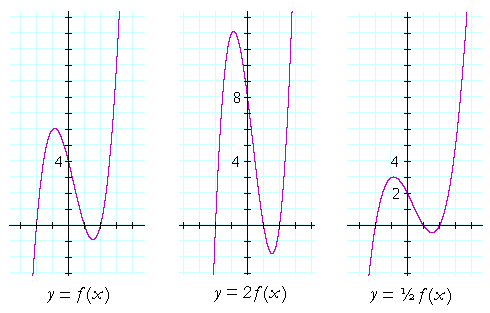
If we multiply f(x) by a number greater than 1 -- as in the graph in the center -- then every y-value is stretched; in that graph, by a factor of 2.
But if we multiply f(x) by a number less than 1 -- as in the graph on the right -- then every y-value is shrunk; in that graph, by a factor of ½.
Next Topic: Rational functions
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2012 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com