Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

TWO RIGHT ANGLES
Book I. Propositions 13 and 14
Straight angles. Supplementary angles.
WE KNOW THAT WHEN A STRAIGHT LINE EB stands on another straight
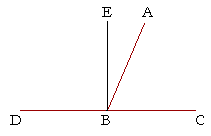
line and makes the adjacent angles equal, then we have two right angles. But it should be obvious that when any straight line stands on another, then the adjacent angles ABC, ABD are together equal to two right angles. That is the next proposition.
(The proof will show that the two right angles CBE, EBD
are equal to the three angles CBA, ABE, EBD;
but angles CBA, ABD are also equal to those three angles;
therefore CBA, ABD are equal to the two right angles.)
PROPOSITION 13. THEOREM
| When a straight line that stands on another straight line makes two angles, either it makes two right angles, or it makes angles that together are equal to two right angles. | |
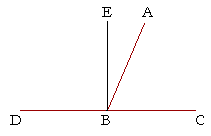
| Let the straight line AB stand on the straight line CD and make the | |
| two angles CBA, ABD; | |
| then either angles CBA, ABD are two right angles, or together they are | |
| equal to two right angles. | |
 |
|
| For if angle CBA is equal to angle ABD, then they are two right | |
| angles. | (Definition 3) |
| But if they are not equal, then draw BE from the point B at right angles | |
| to CD; | (I. 11) |
| therefore angles CBE, EBD are two right angles. | |
| Now, since angles | |
| CBA, ABE are equal to angle CBE, | |
| to each of those join the right angle EBD; | |
| therefore the three angles | |
| CBA, ABE, EBD are equal to angles CBE, EBD. | (Axiom 2) |
 |
|
| And, since angles | |
| ABE, EBD are equal to angle ABD, | |
| to each of those join angle CBA; | |
| therefore the three angles | |
| CBA, ABE, EBD are equal to angles CBA, ABD. | (Axiom 2) |
| But we have shown that angles CBE, EBD are equal to those same three angles; | |
| and things that are equal to the same thing are equal to one another; | |
| (Axiom 1) | |
| therefore angles | |
| CBA, ABD are equal to angles CBE, EBD. | |
| But CBE, EBD are two right angles; | |
| therefore angles CBA, ABD are together equal to two right angles. | |
| Therefore, when a straight line that stands on another straight line etc. Q.E.D. | |
| Corollary 1. When two straight lines intersect one another, the four angles they make are together equal to four right angles. | 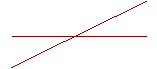 |
| Corollary 2. Therefore when any number of straight lines intersect at one point, all the angles they make are together equal to four right angles. | 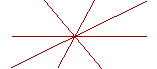 |
![]()
The hypothesis of Proposition 13 is that the straight line which stands on the other makes two angles. But how could it not make two angles? If it stood at the extremity of the line. In that case, it would make only one angle.
When it does not stand at the extremity, however, then the angles formed are equal to two right angles. Conversely -- if angles
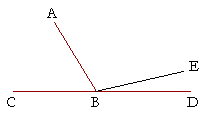
ABC, ABD together are equal to two right angles, then BD is in a straight line with CB.
This is Proposition 14. But there is no previous proposition or definition that gives a criterion for two straight lines being in a straight line. This proposition is the criterion. Therefore, it can be proved only by the indirect method.
Thus, if we assume that BD is not in a straight line with CB, then we may assume that BE is, because the straight line CB may be extended in a straight line. But this leads to the conclusion that angle ABE is equal to angle ABD, the smaller to the larger; which is absurd. (Can you show that?) It follows, then, that BD is the only straight line that is in a straight line with CB.
PROPOSITION 14. THEOREM
| If two straight lines are on opposite sides of a given straight line, and, meeting at one point of that line they make the adjacent angles equal to two right angles, then the two straight lines are in a straight line with one another. | |
| Let two straight lines CB, BD be on opposite sides of the straight line AF, meeting at the point B, and let the adjacent angles ABC, ABD be equal to two right angles; then BD will be in a straight line with CB. |
|
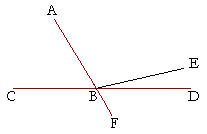 |
|
| For if BD is not in a straight line with CB, let BE be in a straight line with CB. | |
| Then, since the straight line AB stands on the (supposed) straight line CBE, | |
| it makes the adjacent angles ABC, ABE equal to two right angles. | (I. 13) |
| But angles ABC, ABD are also equal to two right angles. | (Hypothesis) |
| Therefore angles ABC, ABE are equal to angles ABC, ABD. | |
| (Postulate 4 and Axiom 1) | |
| From each pair take away angle ABC; | |
| then the remaining angle ABE is equal to the remaining angle ABD, | |
| (Axiom 3) | |
| the smaller to the larger -- which is absurd. | |
| Therefore BE is not in a straight line with CB. | |
| In the same manner we can prove that neither is any other straight line except BD. | |
| Therefore, if two straight lines etc. Q.E.D. | |
Straight angles. Supplementary angles.
An angle in plane geometry is strictly less than two right angles.
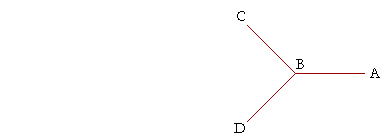
We do not think of angles ABC, CBD together as one angle. The angle we call angle ABD is the obtuse angle ABD, which is less than two right angles.
If CD is a straight line, then, and AB meets it, then in classical
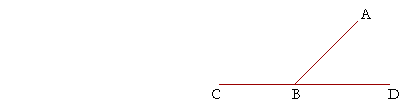
geometry we do not call CBD an angle. It has become a feature of of modern treatments, however, to call CBD a straight angle.
A straight angle is one whose sides are in a straight line
with one another.
Given that concept, Proposition 14 is then both obvious and trivial. It was very likely with that in mind that a straight angle originated .
When two angles together are equal to a straight angle -- to two right angles -- we say that they are supplements of one another, or that they are supplementary angles. Thus angle ABC above is the supplement of angle ABD, and vice-versa. It will be left to Problem 5 to prove the simple theorem:
Angles that are supplements of the same angle are equal to one another.
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com