Adding algebraic fractions: Level 2
Problem 8.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | 1 x |
+ | 2 3x |
= | 3 + 2 3x |
= | 5 3x |
b) | 3 2x |
− | 4 2x2 |
= | 3x − 4 2x2 |
| c) | 1 (x + 1)2 |
+ | 2 (x + 1) |
= | 1 + 2(x + 1) (x + 1)2 |
= | 1 + 2x + 2 (x + 1)2 |
= | 2x + 3 (x + 1)2 |
| d) | 6 x(x − 1) |
+ | 2 x(x − 2) |
= | 6(x − 2) + 2(x − 1) x(x − 1)(x − 2) |
| = | 6x − 12 + 2x − 2 x(x − 1)(x − 2) |
||||
| = | _8x − 14_ x(x − 1)(x − 2) |
||||
| Example 7. Add | 4 x2 − 25 |
− | 3 x2 − 6x + 5 |
Note that we tend to say "add" in algebra, even though the operation is subtraction.
Solution. To construct the LCM of the denominators, we must first factor the denominators. In fact, whenever we add fractions in algebra, the denominators must be composed of factors.
| 4 x 2 − 25 |
− | 3 x2 − 6x + 5 |
= | _4_ (x + 5)(x − 5) |
− | _3_ (x − 5)(x − 1) |
| = | 4(x − 1) − 3(x + 5) (x + 5)(x − 5)(x − 1) |
|||||
| = | _4x − 4 − 3x − 15_ (x + 5)(x − 5)(x − 1) |
|||||
| = | __x − 19__ (x + 5)(x − 5)(x − 1) |
|||||
Problem 9. Add. First factor each denominator.
| a) | x 2 |
+ | _5_ 2x + 2 |
= | x 2 |
+ | _5_ 2(x + 1) |
| = | x(x + 1) + 5 2(x + 1) |
||||||
| = | x2 + x + 5 2(x + 1) |
||||||
| b) | 1 x2 − x |
+ | 2 x |
= | _1_ x(x − 1) |
+ | 2 x |
| = | 1 + 2(x − 1) x(x − 1) |
||||||
| = | 1 + 2x − 2 x(x − 1) |
||||||
| = | 2x − 1 x(x − 1) |
||||||
| c) | 2 x + 3 |
+ | 12 x2 − 9 |
= | 2 x + 3 |
+ | __12__ (x + 3)(x − 3) |
| = | 2(x − 3) + 12 (x + 3)(x − 3) |
||||||
| = | 2x − 6 + 12 (x + 3)(x − 3) |
||||||
| = | ___2x + 6___ (x + 3)(x − 3) |
||||||
| = | __ 2(x + 3) __ (x + 3)(x − 3) |
||||||
| = | _2_ x − 3 |
||||||
| d) | ___6___ x2 + 5x + 6 |
+ | ___2___ x2 − x − 6 |
= | ___6___ (x + 2)(x + 3 ) |
+ | ___ 2___ (x + 2)(x − 3) |
| = | 6(x − 3) + 2(x + 3) (x + 2)(x + 3)(x − 3) |
||||||
| = | _ 6x − 18 + 2x + 6 _ (x + 2)(x + 3)(x − 3) |
||||||
| = | _____8x − 12_____ (x + 2)(x + 3)(x − 3) | ||||||
| = | ___ 4(2x − 3) ___ (x + 2)(x + 3)(x − 3) | ||||||
Factor the numerator to see if anything might cancel.
| e) | ___3___ x2 − 7x + 10 |
− | __2__ x2 − 25 |
= | ___3___ (x − 2)(x − 5) |
− | ___ 2___ (x + 5)(x − 5) |
| = | 3(x + 5) − 2(x − 2) (x − 2)(x − 5)(x + 5) |
||||||
| = | _ 3x + 15 − 2x + 4 _ (x − 2)(x − 5)(x + 5) |
||||||
| = | ___ __x + 19__ ___ (x − 2)(x − 5)(x + 5) |
||||||
| f) | ___7___ 3x2 − 5x + 2 |
− | ___4___ 3x2 + x − 2 |
= | ___7___ (3x − 2)(x − 1) |
− | ___ 4___ (3x − 2)(x + 1) |
| = | 7(x + 1) − 4(x − 1) (3x − 2)(x − 1)(x + 1) |
||||||
| = | _ 7x + 7 − 4x + 4_ (3x − 2)(x − 1)(x + 1) |
||||||
| = | ___ __3x + 11__ ___ (3x − 2)(x − 1)(x + 1) |
||||||
Example 8. Symmetrically, if the numerator of a fraction is a sum, then we can rewrite that fraction as a sum of fractions:
| a + b + c d |
= | a d |
+ | b d |
+ | c d |
. |
Problem 10. Rewrite each of the following as a sum of fractions, and simplify.
| a) | 1 + 2 + 3 6 |
= | 1 6 |
+ | 2 6 |
+ | 3 6 |
= | 1 6 |
+ | 1 3 |
+ | 1 2 |
| b) | 2n2 − 4n + 1 n2 |
= | 2n2 n2 |
− | 4n n2 |
+ | 1 n2 |
= | 2 | − | 4 n |
+ | 1 n2 |
| c) | x³ + 4x2 + 2 2x5 |
= | x³ 2x5 |
+ | 4x2 2x5 |
+ | 2 2x5 |
= | 1 2x2 |
+ | 2 x3 |
+ | 1 x5 |
| d) | x − 1 x + 1 |
= | x x + 1 |
− | 1 x + 1 |
| Example 9. Simplify | 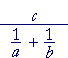 |
| Solution. | 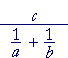 |
= | 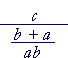 |
|||
| = | c · | ab b + a |
(Definition of division) | |||
| = | cab b + a |
or | abc a + b |
|||
Problem 11. Simplify.
| a) | 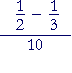 |
= | 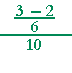 |
= | 1 6 |
· | 1 10 |
= | 1 60 |
| b) | 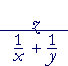 |
= | 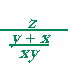 |
= z · | xy y + x |
= | zxy y + x |
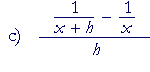 |
= | x − (x + h) (x + h)x |
· | 1 h |
|
| = | x − x − h (x + h)x |
· | 1 h |
||
| = | −h (x + h)x |
· | 1 h |
||
| = | − | 1 (x + h)x |
, on canceling the h's. | ||
| d) | 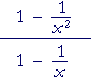 |
= | 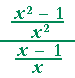 |
= | (x + 1)(x − 1) x2 |
· | x x − 1 |
= | x + 1 x |
Or, on recognizing the numerator as the Difference of Two Squares:
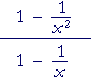 |
= | 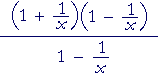 |
= 1 + | 1 x |
= | x + 1 x |
| e) | 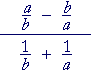 |
= | 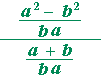 |
||
| = | (a + b)(a − b) ba |
· | ba a + b |
||
| = | a − b | ||||
Next Lesson: Equations with fractions
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com