32
THE PYTHAGOREAN DISTANCE FORMULA
The distance of a point from the origin
The distance between any two points
A proof of the Pythagorean theorem
BASIC TO TRIGONOMETRY and calculus is the theorem that relates the squares drawn on the sides of a right-angled triangle. Credit for proving the theorem goes to the Greek philosopher Pythagoras, who lived in the 6th century B. C.
Here is the statement of the theorem:
In a right triangle the square drawn on the side opposite the right angle
is equal to the squares drawn on the sides that make the right angle.
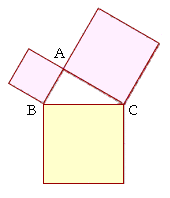
That means that if ABC is a right triangle with the right angle at A, then the square drawn on BC opposite the right angle, is equal to the two squares together on CA, AB.
In other words, if it takes one can of paint to paint the square on BC, then it will also take exactly one can to paint the other two squares.
The side opposite the right angle is called the hypotenuse ("hy-POT'n-yoos"; which literally means stretching under).
Algebraically, if the hypotenuse is c, and the sides are a, b:
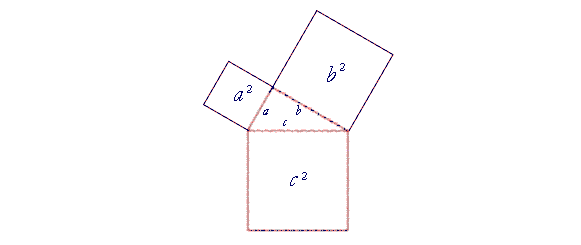
a2 + b2 = c2.
For a proof, see below.
Problem 1. State the Pythagorean theorem in words.
In a right triangle the square on the side opposite the right angle will equal the squares on the sides that make the right angle.
Problem 2. The right triangle below has sides, a, b, c .
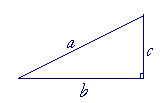
Which of the following is correct?
a) a2 + b2 = c2
b) a2 + c2 = b2
c) a2 = b2 + c2
d) c2 = b2 + a2
c) is correct.
Problem 3. Let c be the hypotenuse of a right triangle. Calculate its length when the sides are as follows.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
a) a = 5 cm, b = 12 cm.
| c2 | = | 52 + 122 | |
| = | 25 + 144 | ||
| = | 169. | ||
| Therefore, c | = | ||
| = | 13 cm, | ||
| on simplifying the radical. | |||
b) a = 3 cm, b = 6 cm.
| c2 | = | 32 + 62 | |
| = | 9 + 36 | ||
| = | 9(1 + 4) | ||
| = | 9 · 5. | ||
| Therefore, c | = | ||
| = | |||
Since 9 is a square number, and a common factor of 9 and 36, then we may anticipate simplifying the radical by writing 9 + 36 = 9(1 + 4) = 9 · 5.
We could, of course, have written 9 + 36 = 45 = 9 · 5. But that first wipes out the square number 9. We then have to bring it back.
The distance d of a point (x, y) from the origin
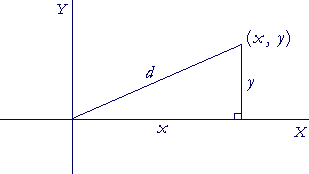
According to the Pythagorean theorem and the meaning of the rectangular coördinates (x, y),
d 2 = x2 + y2.
Therefore,
![]()
"The distance of a point from the origin
is equal to the square root of the
sum of the squares of the coördinates."
Example 1. How far from the origin is the point (4, −5)?
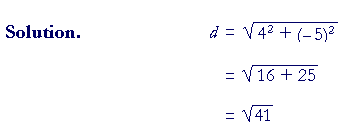
Problem 4. How far from the origin is the point (−5, −12)?
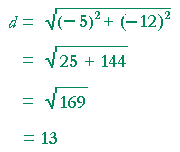
The distance between any two points
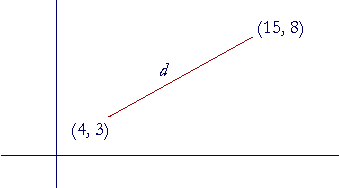
How far is it from (4, 3) to (15, 8)?
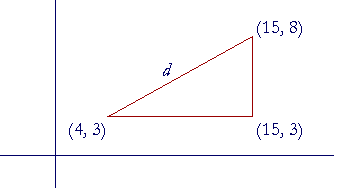
Consider the distance d as the hypotenuse of a right triangle. Then according to Lesson 31, Problem 4, the coördinates at the right angle are (15, 3).
Therefore, the horizontal leg of that triangle is simply the distance from 4 to 15: 15 − 4 = 11.
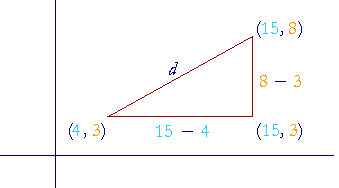
The vertical leg is the distance from 3 to 8: 8 − 3 = 5.
Therefore,
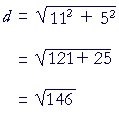
To find a formula, let us use subscripts and label the two points as
(x1, y1) ("x-sub-1, y-sub-1") and (x2, y2) ("x-sub-2, y-sub-2") .
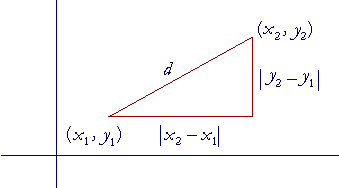
The subscript 1 labels the coördinates of the first point; the subscript 2 labels the coördinates of the second. We write the absolute value because distance is never negative.
Here then is the Pythagorean distance formula between any two points:
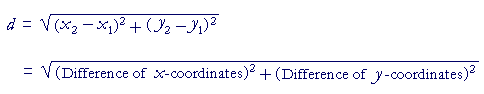
It is conventional to denote the difference of x-coördinates by the symbol Δx ("delta-x"):
Δx = x2 − x1
Similarly,
Δy = y2 − y1
Therefore,
![]()
Example 2. Calculate the distance between the points (1, 3) and (4, 8).
| Solution. | Δx | = | 4 − 1 = 3. |
| Δy | = | 8 − 3 = 5. | |
Therefore,
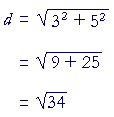
Note: It does not matter which point we call the first and which the second. Alternatively,
| Δx | = | 1 − 4 = −3. | |
| Δy | = | 3 − 8 = −5. | |
But (−3)2 = 9, and (−5)2 = 25. The squares will always be positive.
Example 3. Calculate the distance between the points (−8, −4) and (1, 2).
| Solution. | Δx | = | 1 − (−8) = 1 + 8 = 9. |
| Δy | = | 2 − (−4) = 2 + 4 = 6. | |
Therefore,
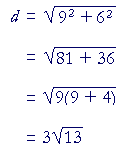
Problem 5. Calculate the distance between (2, 5) and (8, 1)
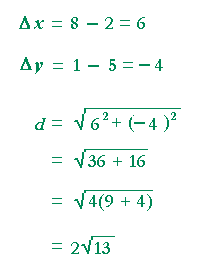
Problem 6. Calculate the distance between (−11, −6) and (−16, −1)
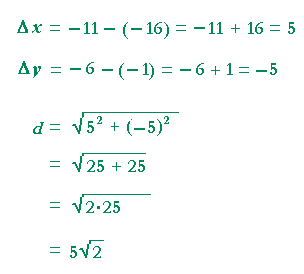
A proof of the Pythagorean theorem
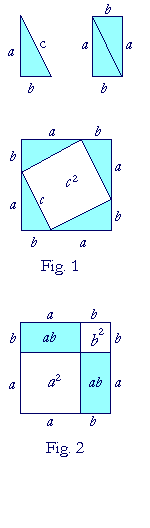
Let a right triangle have sides a, b, and hypotenuse c. And let us arrange four of those triangles to form a square whose side is a + b. (Fig. 1)
Now, the area of that square is equal to the sum of the four triangles, plus the interior square whose side is c.
Two of those triangles taken together, however, are equal to a rectangle whose sides are a, b. The area of such a rectangle is a times b: ab. Therefore the four triangles together are equal to two such rectangles. Their area is 2ab.
As for the square whose side is c, its area is simply c2. Therefore, the area of the entire square is
c2 + 2ab. . . . . . . (1)
At the same time, an equal square with side a + b (Fig. 2)
is made up of a square whose side is a, a square whose side is b, and two rectangles whose sides are a, b. Therefore the area of that square is
a2 + b2 + 2ab.
But this is equal to the square formed by the triangles, line (1):
a2 + b2 + 2ab = c2 + 2ab.
Therefore, on subtracting the two rectangles 2ab from each square, we are left with
a2 + b2 = c2.
That is the Pythagorean theorem.
Next Lesson: The equation of a straight line
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
