2
THE RATIO OF TWO
NATURAL NUMBERS
The ratio of a smaller number to a larger
THE STUDENT WHO HAS DONE THE previous lesson can begin to appreciate that there is always a name for how any two natural numbers are related. 7 is half of 14. 24 is three times 8. 10 is two thirds of 15. Those names are called their ratio. Ratio is the spoken language of arithmetic.
DEFINITION. The ratio of two natural numbers is their relationship with respect to relative size, which we can always name. Specifically, we can say that one number is a multiple of the other (so many times it), a part of it, or parts of it.
(Topic 1. Cf. Euclid, VII. Def. 20.)
Example 1. Multiple What ratio has 15 to 5?
Answer. 15 is three times 5.
That is the ratio -- the relationship -- of 15 to 5.
We do not answer "3 to 1," because we want to name the ratio of 15 to 5 explicitly. It is true that 15 has the same ratio to 5 that 3 has to 1. 3 is three times 1, just as 15 is three times 5.
The two numbers in a ratio are called the terms; the first term and the second.
Notice that we answer with a complete sentence beginning with the first term and ending with the second: "15 is three times 5." For, a ratio is a relationship.
Example 2. Part What ratio has 5 to 15?
Answer. 5 is the third part of 15.
That is called inverse ratio of 15 to 5. The terms are exchanged.
Example 3. Parts What ratio has 10 to 15?
Answer. 10 is two thirds of 15.
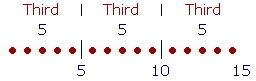
Those are the three types of ratio: One number is a multiple of the other (so many times it), a part of it, or parts of it.
Problem 10. What ratio have the following? Answer with a complete sentence beginning with the first term.
a) 2 to 10? 2 is the fifth part of 10.
| b) 10 to 2? | 10 is five times 2. A larger number is always so many times a smaller. |
c) 7 to 1? 7 is seven times 1.
d) 1 to 7? 1 is the seventh part of 7.
e) 25 to 100? 25 is the fourth part of 100.
f) 75 to 100? 75 is three fourths of 100.
g) 12 to 6? 12 is two times 6, or twice as much as 6, or double 6.
h) 6 to 12? 6 is half of 12.
i) 40 to 8? 40 is five times 8.
j) 24 to 6? 24 is four times 6.
k) 6 to 24? 6 is the fourth part of 24.
l) 10 to 1? 10 is ten times 1.
m) 1 to 10? 1 is the tenth part of 10.
The ratio of a smaller number to a larger
2 to 3
We can always name the ratio of any smaller number to a larger simply by letting each number say its name. Let the smaller number say its cardinal name -- One, two, three, . . . Let the larger number say its ordinal name -- third, fourth, fifth . . . .
Example 4. What ratio has 2 to 3?
Answer. "2 is two thirds of 3."
2 says its cardinal name, "two." 3 says its ordinal name, "third."
Example 5. What ratio has 4 to 5?
Answer. "4 is four fifths of 5." Each number says its name.
To see this, consider that 1 is one fifth of 5:
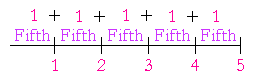
2 is two fifths of 5.
3 is three fifths of 5.
4 is four fifths of 5.
Each number says its name.
Problem 11. What ratio has
a) 5 to 8? 5 is five eighths of 8.
b) 3 to 4? 3 is three fourths of 4.
c) 2 to 9? 2 is two ninths of 9.
c) 99 to 100? 99 is ninety-nine hundredths of 100.
What ratio has 8 to 12? While it is correct to say that 8 is eight twelfths of 12, we will see how to express that ratio with the smallest numbers that have that ratio, that is, with the lowest terms. (Lesson 3: The theorem of the common divisor.)
A mixed number of times
By a mixed number of times, we mean a whole number of times plus a part.
Example 6. How much is two and a half times 8?
Answer. "Two and a half times 8" means
Two times 8 plus half of 8.
Two times 8 is 16. Half of 8 is 4. 16 plus 4 is 20.
Example 7. A cheese sells for $6 a pound, and you buy three and a half pounds. How much do you pay?
| Answer. | Three pounds cost $18. |
| Half a pound costs $3. | |
| You pay $21. | |
That is, "Three and a half times 6" means
Three times 6 plus half of 6.
18 + 3 = 21.
This is a mixed number of times: A whole number of times plus a part.
Example 8. How much is five and a quarter times 8?
| Answer. | "Five times 8 is 40. |
| "A quarter (or a fourth) of 8 is 2. | |
| "40 + 2 = 42." | |
Problem 12. How much is
a) Two and a half times 40? 80 + 20 = 100
b) One and a half times 12? 12 + 6 = 18
c) One and a quarter times 20? 20 + 5 = 25
d) Two and a quarter times 8? 16 + 2 = 18
e) Three and a half times 10? 30 + 5 = 35
f) Five and a third times 6? 30 + 2 = 32
g) Two and a quarter times 100? 200 + 25 = 225
h) Two and three quarters times 100? 200 + 75 = 275
Mixed ratio
Ratio and division
We just saw that "20 is two and a half times 8." That statement expresses the ratio of 20 to 8. It is called a mixed ratio. In a mixed ratio, the larger number is a multiple of the smaller number, plus a part or parts of the smaller number.
Example 9. What ratio has 25 to 10?
Answer. We can decompose 25 into a multiple of 10 plus a remainder:
25 = 20 + 5.
25 is made up of two 10's, plus a remainder of 5. The remainder 5 is a part of 10, namely half. Therefore we say,
"25 is two and a half times 10."
Two times 10 is 20; half of 10 is 5; 20 plus 5 is 25.
We always say that a larger number is so many times a smaller number. 25 is two and a half times 10.
Example 10. What ratio has 13 to 3? That is, 13 is how many times 3?
To answer, we can divide 13 by 3.
13 ÷ 3 = 4 R 1.
13 is made up of four 3's with remainder 1.
The remainder 1 is a part of 3 -- it is the third part. We say,
"13 is four and a third times 3."
Notice again: We always say that a larger number is so many times a smaller.
Example 11. What ratio has 50 to 40?
Answer. 50 is one and a quarter times 40.
For, 50 contains 40 one time with remainder 10.
The remainder 10 is a quarter of 40. Therefore,
50 is one and a quarter times 40.
We now see that we can always express in words the relationship -- the ratio -- of any two natural numbers.
We also see the relationship between ratio and division. The quotient of two numbers indicates the ratio of those numbers. The ratio of 15 to 5, for example, is indicated by 15 ÷ 5 = 3. This implies:
15 = 3 × 5.
"15 is three times 5."
The traditional notation for ratio is 15 : 3, which is the divison sign ÷ but without the bar.
Problem 13. Express each ratio. (The larger number is how many times the smaller number?)
a) 45 to 10? 45 is four and a half times 10.
b) 20 to 8? 20 is two and a half times 8.
c) 22 to 4? 22 is five and a half times 4.
d) 5 to 2? 5 is two and a half times 2.
e) 7 to 2? 7 is three and a half times 2.
f) 13 to 2? 13 is six and a half times 2.
g) 5 to 4? 5 is one and a quarter times 4.
h) 9 to 4? 9 is two and a quarter times 4.
i) 11 to 4? 11 is two and three quarters times 4.
j) 11 to 3? 11 is three and two thirds times 3.
k) 44 to 6? 44 is seven and a third times 6.
Finally, then, we see that we can always express in words the ratio of any two natural numbers.
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2020 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
