Appendix 4
TWO THEOREMS
The distributive property of multiplication
The order property
IN ALGEBRA, distribution is an axiom. But in arithmetic we define multiplication, which algebra does not, and therefore we can prove the distributive property. It is only because it is true in arithmetic that the distributive axiom of algebra will apply to arithmetic. The same can be said of the order property of multiplication.
As for the distributive property, here is an example:
| 3 × (20 + 4) | = | 3 × 20 + 3 × 4. |
| Or, the other way around: | ||
| 3 × 20 + 3 × 4 | = | 3 × (20 + 4). |
| Three 20's + Three 4's | = | Three 24's. |
Looked at in that way, it is the theorem of adding the same multiple of numbers.
The third multiple of 20 added to the third multiple of 4
is equal to the third multiple of 20 + 4.
Here is the theorem:
| 1. |
The sum of the same multiple of numbers will be that same multiple of the sum of those numbers. |
| Euclid, V, 1. | |
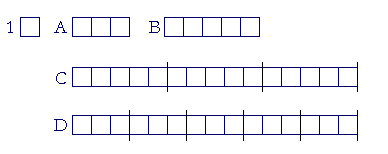
Let the number A be a multiple of the number C, and let the number B be the same multiple of the number D.
Then the sum of A and B will also be that multiple of the sum of C and D.
For, since A is the same multiple of C that B is of D, there are as many numbers in A equal to C as there are in B equal to D.

Therefore divide A into the numbers G, H, I each equal to C,
and divide B into the numbers J, K, L each equal to D;
A and B will then be divided the same number of times..
Now, since G is equal to C, and J equal to D, the sum of G and J is equal to the sum of C and D.
For the same reason, the sum of H and K, and the sum of I and L, are also equal to the sum of C and D.
As many numbers, then, as there are in A equal to C, the sum of A and B will be composed of the sum of C and D that many times.
Therefore, whatever multiple A is of C, the sum of A and B is that multiple of the sum of C and D.
Which is what we wanted to prove.
*
We can now prove the order property of multiplication. Specifically, for example:
| Three 5's | = | 5 + 5 + 5 |
| = | Five 1's + Five 1's + Five 1's. | |
Each Five is the same multiple of 1, namely the fifth. Therefore the sum of those same multiples of 1 will be that multiple of the sum of the 1's. (Theorem 1.) It will be the fifth multiple of 1 + 1 + 1. That is, it will
= Five 3's.
Here is the theorem:
| 2. | If two numbers multiply one another, the products will equal one another. |
| Euclid, VII, 16. | |
Let the number A multiply the number B producing C, and let B multiply A producing D.
Then C is equal to D.
For when A multiplies B producing C, then C is the repeated addition of B according to the 1's in A.
But each B is a number of 1's. Each B is the same multiple of 1.
![]()
Therefore, the sum of those same multiples of 1 will be that multiple of the sum of the 1's. (Theorem 1.)
![]()
That multiple is the number of 1's in B. And the sum of the 1's is A because A is the number of times that B is repeatedly added.
But that is equal to D -- the repeated addition of A according to the number of 1's in B.
Therefore, if two numbers multiply one another, the products will equal one another.
Which is what we wanted to prove.
That is the proof for natural numbers. A proof based on the general definition of multiplication and that includes fractions, is in Lesson 27.
![]()
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com