Appendix 3
THEORETIC ARITHMETIC
Triangular numbers
Square numbers
The sum of consecutive squares
The sum of consecutive cubes
A formula for the triangular numbers
The sum of consecutive squares
Section 2: The sum of consecutive cubes
IN THIS TOPIC we will look at numbers themselves, not just their symbols — 1, 2, 3, 4. By doing so we will see unexpected structures that are inherent in the natural numbers.
Here is a number in the form of a triangle:

This is number 10. (Count them.) Since 10 can be pictured in this way, we call 10 a triangular number.
Now, how do we generate a triangular number? We begin with 1:
![]()
We say that 1 is the first triangular number. To form the next, we add 2:
So the next triangular number is 3. The number we add to the previous triangular number is called the gnomon (NOH-mon). We added the gnomon 2 to 1.
To form the next triangular number, we add the gnomon 3:
![]()
It produces the next triangular number, 6.
To form the next, we add 4:

And so the first four triangular numbers are 1, 3, 6, 10. Each one is the sum of consecutive numbers.
| 1. | ||
| 1 + 2 | = | 3. |
| 1 + 2 + 3 | = | 6. |
| 1 + 2 + 3 + 4 | = | 10. |
Problem 1. Write the first ten triangular numbers.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
1, 3, 6, 10, 15, 21, 28, 36, 45, 55.
The difference between consecutive triangles increases by 1.
A formula for the triangular numbers
We will now show that a triangular number -- the sum of consecutive numbers -- is given by this algebraic formula:
½n(n + 1),
where n is the last number in the sum. (For example, n = 4 in the last sum above.)
To see that, look at this oblong number, in which the base is one more than the height:

An oblong number is the product of a number with its successor, which is the one after. Algebraically, it has the form
n(n + 1).
In this one, the height n is 4; that is, this oblong number is 4 × 5 = 20.
But an oblong is composed of two equal triangles:
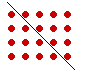
Therefore each triangle is half of the oblong. Each one is
The sum of consecutive numbers is equal to half the product of the
last number in the sum with its successor.
Example. Find the sum of the first 50 numbers -- that is, find the 50th triangular number.
Solution. In the formula, we will put n = 50. Then n + 1 = 51. Therefore the sum is
½(50 × 51) = ½(2550) = 1275.
Problem 2. What is the 200th triangular number?
½(200 × 201) = ½(40,200) = 20,100.
Note that the sum of consecutive even numbers --
2 + 4 + 6 + 8
-- is the oblong itself.
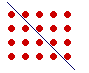
2 + 4 + 6 + 8 = 4 × 5 =20.
For,
2 + 4 + 6 + 8 = 2 × (1 + 2 + 3 + 4).
Problem 3. Find the sum of the first 50 even numbers.
50 × 51 = 2550.
For the sum of consecutive odd numbers, see Appendix 2.
Square numbers

Just as a triangular number is a number that can appear as a triangle, so a square number can take the form of a square. 25 is a square number.
Now, how are square numbers related to triangular numbers?
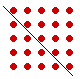
Every square is composed of two consecutive triangles.
Triangles: 1 3 6 10 15 21 28 . . .
| 1 + 3 | = | 4. |
| 3 + 6 | = | 9. |
| 6 + 10 | = | 16. |
| 10 + 15 | = | 25. |
| 15 + 21 | = | 36. |
We will now use this to determine --
The sum of consecutive squares
Since a square number is composed of triangular numbers, then a sum of squares will be a sum of triangles.
| 1 + 4 + 9 | = | 1 + 1 + 3 + 3 + 6 |
| = | 1 + 1 + 1 + 2 + 1 + 2 + 1 + 2 + 3 | |
| = | 5 × 1 + 3 × 2 + 1 × 3. |
Now -- if there were an equal number of 1's, 2's, and 3's,
then the sum of those 3 squares would be a multiple of the 3rd triangle, 1 + 2 + 3. However, some multiple of the triangle will equal a multiple of the squares. They have a common multiple.
The sum of the squares is 14. The triangular number is 6.
14 = 2 × 7. 6 = 2 × 3.
Their lowest common multiple is 2 × 3 × 7 = 42. (Lesson 33.)
Therefore if we multiply the sum of the squares by 3, and the triangular number by 7, then
3 × (1 + 4 + 9) = 7 × (1 + 2 + 3).
3 times the sum of consecutive squares
is equal to an odd multiple
of the sum of consecutive numbers.
We will now see that that is always the case. To construct their common multiple, the squares will be multiplied by 3, and the triangle by the next odd number.
Consider the squares 1 + 4 and the triangular number 1 + 2. Then
3 × (1 + 4) = 5 × (1 + 2).
Consider the sum of four squares 1 + 4 + 9 + 16 and the fourth triangle 1 + 2 + 3 + 4.
The sum of the squares is 30. The triangular number is 10. Although 30 is itself a common multiple, if we multiply the squares again by 3, and the triangle by 9, then
3 × (1 + 4 + 9 + 16) = 9 × (1 + 2 + 3 + 4).
If we have only the first square 1, then 3 × 1 equals 3 times the first triangular number, which is also 1.
And so if we multiply each sum of squares by 3, this is what we have found so far.
| The number of terms n in the sum of squares | The multiplier of the triangular number with n terms |
|---|---|
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
Those multipliers are the sequence of odd numbers beginning with 3. Each odd number is 1 more than twice the number of terms; algebraically, 2n + 1.
The question is: To produce their common multiple, why are the squares always multiplied by 3? And why is the triangle always multiplied by the next odd number?
To try to answer that, consider these prime factorizations.
| Number of terms n | Sum of squares | Triangle |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 5 | 3 |
| 3 | 14 = 2×7 | 6 = 2×3 |
| 4 | 30 = 2×3×5 | 10 = 2×5 |
| 5 | 55 = 5×11 | 15 = 3×5 |
| 6 | 91 = 7×13 | 21 = 3×7 |
| 7 | 140 = 2×2×5×7 | 28 = 2×2×7 |
| 8 | 204 = 2×2×3×17 | 36 = 2×2×3×3 |
| 9 | 285 = 3×5×19 | 45 = 3×3×5 |
| 10 | 385 = 5×7×11 | 55 = 5×11 |
Inspection reveals the following.
If n is in this remainder class modulo 3: 1, 4, 7, 10, . . ., then the sum of squares has all the factors of the triangle.
In that remainder class, 2n + 1 is a multiple of 3. And a third of 2n + 1 is a prime factor of the squares. It is the prime factor missing from the triangle.
Therefore, when the squares are multiplied by 3, then 2n + 1 itself will be a factor. When the triangle is mutliplied by 2n + 1, it will then have all the factors of 3 times the squares.
In the other two remainder classes, each triangle has a factor 3 that the squares do not. The only factor the squares have which the triangle does not, is 2n + 1. Their common multiple follows.
And so we have found this algebraic formula for the sum of consecutive squares.
3(12 + 22 + 32 + . . . + n2) = (2n + 1)(1 + 2 + 3 + . . . + n).
Or, according to the formula for the triangular numbers:
| 12 + 22 + 32 + . . . + n2 | = | (2n + 1)n(n + 1) 6 |
. |
*
Section 2: The sum of consecutive cubes
![]()
Introduction | Home | Table of Contents
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
