Lesson 18
SOLVING PROPORTIONS
This Lesson follows from Lesson 17, where we saw that a proportion is a statement involving four numbers, called the terms.
1st : 2nd = 3rd : 4th.
A problem in proportions consists of being given three of the terms; we are asked to name the fourth.
7 : 21 = 9 : ?
That is what it means to solve a proportion.
What is taught in most textbooks these days as ratio and proportion, is not. It is algebra. The student is taught to represent a ratio as a fraction, write the letter x for the unknown term, cross-multiply and solve an equation. That is an algebraic calculator.
Ratio and proportion, on the other hand, is purely arithmetical and requires simple understanding. It is therefore educational.
In this Lesson, we will answer the following:
- In a proportion, which are the corresponding terms?
- What is the theorem of the alternate proportion?
- What is the theorem of the same multiple?
- What does "out of" indicate?
- How do we find a percent by the method of proportions?
- What is a mixed ratio?
- What does it mean to express a relationship between numbers in the language of ratio?
| 1. | In a proportion -- | |
| 1st : 2nd = 3rd : 4th | ||
| -- which are the corresponding terms? | ||
| The 1st and 3rd terms, the 2nd and the 4th. | ||
1 : 2 = 5 : 10
1 is called the first term of the proportion, 2 is the second term, 5 is the third, and 10, the fourth.
We say that 5 corresponds to 1, and 10 corresponds to 2.
| 2. | What is the theorem of the alternate proportion? |
|
"If four numbers are proportional, then the corresponding terms are also proportional." |
|
| If | |
| 1st : 2nd = 3rd : 4th | |
| then alternately, | |
| 1st : 3rd = 2nd : 4th | |
Example 1. 1 : 2 = 5 : 10.
(1 is half of 2; 5 is half of 10.)
Alternately:
1 : 5 = 2 : 10
(1 is a fifth of 5; 2 is a fifth of 10.)
Example 2.
Directly :
12 : 36 = 2 : 6. (Why?)
Alternately:
12 : 2 = 36 = 6. (Why?)
Example 3. Complete this proportion:
5 : 7 = 20 : ?
If we look directly at the ratio of 5 to 7, it is not obvious. But if we look alternately, we see that 5 is a fourth of 20:
5 : 7 = 20 : 28.
And 7 is a fourth of 28.
If we cannot solve a proportion directly, then we can solve it alternately.
Example 4. The theorem of the same multiple. Complete this proportion:
4 : 5 = 12 : ?
Solution. 4 is a third of 12 -- or we could say that 4 has been multiplied by 3. Therefore, 5 also must be multiplied by 3:
4 : 5 = 12 : 15.
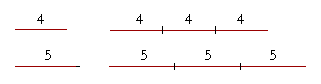
As 4 is to 5, so three 4's are to three 5's.
In fact, as 4 is to 5, so any number of 4's are to an equal number of 5's.
That is called the theorem of the same multiple. It follows directly from the theorem of the alternate proportion.
| 3. | What is the theorem of the same multiple? |
|
"If we multiply two numbers by the same number, then the products will have the same ratio as the numbers we multiplied." |
|
(Euclid, VII. 17.)
We have already seen that a ratio will be preserved if we divide both terms by the same number.
Example 5. Complete this proportion:
6 : 7 = ? : 28
Solution. 7 has been multiplied by 4 to give 28. Therefore, 6 also must be multiplied by 4:
6 : 7 = 24 : 28.
To solve that proportion --
6 : 7 = ? : 28
-- we could say:
"7 goes into 28 four times. Four times 6 is 24."
All the Examples and Problems in this lesson should be simple, mental calculations.
Example 6. Solve this proportion:
2 : 3 = 12 : ?
Solution. "2 goes into 12 six times. Six times 3 is 18."
2 : 3 = 12 : 18.
In fact, consider these columns of the multiples of 2 and 3:
2 3
4 6
6 9
8 12
10 15
12 18
14 21
And so on.
Now, 2 is two thirds of 3. (Lesson 17.) And each multiple of 2 is two thirds of that same multiple of 3:
4 is two thirds of 6.
6 is two thirds of 9.
8 is two thirds of 12.
And so on. In fact, those are the only natural numbers where the first will be two thirds of the second.
Note that each pair have a common divisor. And upon dividing by that divisor, the quotients in every case are 2 and 3. That is the theorem of the common divisor. 2 and 3 are the lowest terms. They are the smallest numbers which have the ratio "two thirds."
Example 7. Name three pairs of numbers such that the first is three fifths of the second.
Solution. The elementary pair are 3 and 5. To generate others, take the same multiple of both: 6 and 10, 9 and 15, 12 and 20, and so on.
Example 8. 27 is three fourths of what number?
Solution. Proportionally:
3 : 4 = 27 : ?
"27 is nine times 3. Nine times 4 is 36."
3 : 4 = 27 : 36.
27 is three fourths of 36.
Only a multiple of 3 can be three fourths of another number, which must be that same multiple of 4.
As 3 is to 4, so any number of 3's are to an equal number of 4's.
Example 9. Solve this proportion:
9 : 45 = 2 : ?
Solution. Here, we must look directly:
9 is a fifth of 45. And 2 is a fifth of 10.
9 : 45 = 2 : 10.
Example 10. Common divisor. Complete this proportion:
12 : 200 = ? : 100.
Solution. Alternately, we see that 200 has been divided by 2. Therefore 12 also must be divided by 2.
12 : 200 = 6 : 100.
Instead of dividing 12 and 200 by 2, we could take half. Half of 200 is 100. Half of 12 is 6.
The Rule of Three
We see that if we know three terms of a proportion, then we can always solve for the fourth. That is called The Rule of Three. We can summarize it as follows.
1st : 2nd = 3rd : 4th.
| • | If the 4th term is unknown and the 3rd term is a multiple or part of the 1st (Example 6), then the 4th must be that same multiple or part of the 2nd. |
| (Similarly if the 3rd term is unknown, and the 4th is a multiple of the 2nd; Example 5) |
|
| • | If the 4th term is unknown and the 2nd term is a multiple or a part of the 1st (Example 9), then the 4th must be that same multiple or part of the 3rd. |
Most importantly, we will apply this rule to find what percent one number is of another.
![]()
As for the theorem of the common divisor, it is what we call the symmetrical version of the theorem of the same multiple. For, this proportion,
6 is to 100 as 12 is to 200,
in which the 3rd and 4th terms appear as doubles of the 1st and 2nd, is logically equivalent to this proportion,
12 is to 200 as 6 is to 100,
in which the 3rd and 4th terms appear as halves of the 1st and 2nd.
Example 11. In a class, the ratio of girls to boys is 3 to 4.
![]()
There are 24 boys. How many girls are there?
Solution. Proportionally,
Girls : Boys = 3 : 4 = ? : 24.
Note that 24 corresponds to the Boys.
Now, 4 goes into 24 six times. Therefore, the number of girls is six times 3: 18.
This is another way to approach Example 7 of the previous Lesson. And the following example is another way to approach Example 8 of that Lesson.
Example 12. The whole is equal to the sum of the parts. In a class, the number of girls is 75% of the number of boys. There are 35 students. How many girls are there and how many boys?
Solution. To say that the girls are 75% -- three quarters -- of the boys,
![]()
is to say that the ratio of girls to boys is 3 to 4. But that means that 3 out of every 7 students are girls (3 + 4 = 7), and 4 out of every 7 are boys.
Therefore form the proportion:
Girls : Total number of students =
3 : 7 = ? : 35.
Since 35 is 5 × 7, the missing term is 5 × 3 = 15.
There are 15 girls. And so there are 20 boys.
At this point, please "turn" the page and do some Problems.
or
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
