border

Table of Contents | Home

Adding algebraic fractions:  Level 2

Back to Section 1

Problem 8.

To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!

  a)    1
x		  +    2 
3x		  =   3 + 2
  3x		  =    5 
3x		     b)     3 
2x		  −    4 
2x2		  =   3x − 4
   2x2
  c)         1     
(x + 1)2		   +       2    
(x + 1)		   =   1 + 2(x + 1)
   (x + 1)2		   =   1 + 2x + 2
   (x + 1)2		  =    2x + 3 
(x + 1)2
  d)         6     
x(x − 1)		  +        2     
x(x − 2)		   =   6(x − 2) + 2(x − 1)
   x(x − 1)(x − 2)
 
    =   6x − 12 + 2x − 2
  x(x − 1)(x − 2)
 
    =       _8x − 14_   
x(x − 1)(x − 2)
  Example 7.   Add          4     
x2 − 25		  −           3        
x2 − 6x + 5

Note that we tend to say "add" in algebra, even though the operation is subtraction.

Solution.   To construct the LCM of the denominators, we must first factor the denominators.  In fact, whenever we add fractions in algebra, the denominators must be composed of factors.

     4     
x 2 − 25		  −           3        
x2 − 6x + 5		   =           _4_       
(x + 5)(x − 5)		  −           _3_       
(x − 5)(x − 1)
 
    =    4(x − 1) − 3(x + 5) 
(x + 5)(x − 5)(x − 1)
 
    =   _4x − 4 − 3x − 15_
(x + 5)(x − 5)(x − 1)
 
    =          __x − 19__      
(x + 5)(x − 5)(x − 1)

Problem 9.   Add.   First factor each denominator.

  a)    x
2		  +    _5_  
2x + 2		   =   x
2		  +     _5_   
2(x + 1)
 
    =   x(x + 1) + 5
   2(x + 1)
 
    =   x2 + x + 5
 2(x + 1)
  b)        1   
x2 − x		  +   2
x		   =      _1_   
x(x − 1)		  +  2
x
 
    =   1 + 2(x − 1)
  x(x − 1)
 
    =   1 + 2x − 2
  x(x − 1)
 
    =    2x − 1 
x(x − 1)
  c)       2   
x + 3		  +      12   
x2 − 9		   =      2   
x + 3		  +      __12__    
(x + 3)(x − 3)
 
    =   2(x − 3) + 12
(x + 3)(x − 3)
 
    =     2x − 6 + 12  
 (x + 3)(x − 3)
 
    =   ___2x + 6___
 (x + 3)(x − 3)
 
    =   __ 2(x + 3) __
 (x + 3)(x − 3)
 
    =     _2_  
 x − 3
  d)      ___6___  
x2 + 5x + 6		  +    ___2___ 
x2 − x − 6		   =       ___6___    
(x + 2)(x + 3 )		  +     ___ 2___   
(x + 2)(x − 3)
 
    =    6(x − 3) + 2(x + 3) 
(x + 2)(x + 3)(x − 3)
 
    =   _ 6x − 18 + 2x + 6 _
(x + 2)(x + 3)(x − 3)
 
    =   _____8x − 12_____
(x + 2)(x + 3)(x − 3)
 
    =     ___ 4(2x − 3) ___  
(x + 2)(x + 3)(x − 3)

Factor the numerator to see if anything might cancel.

  e)      ___3___  
x2 − 7x + 10		  −    __2__ 
x2 − 25		   =       ___3___    
(x − 2)(x − 5)		  −     ___ 2___   
(x + 5)(x − 5)
 
    =    3(x + 5) − 2(x − 2) 
(x − 2)(x − 5)(x + 5)
 
    =   _ 3x + 15 − 2x + 4 _
(x − 2)(x − 5)(x + 5)
 
    =   ___ __x + 19__ ___
(x − 2)(x − 5)(x + 5)
   f)       ___7___   
3x2 − 5x + 2		  −     ___4___  
3x2 + x − 2		   =       ___7___    
(3x − 2)(x − 1)		  −      ___ 4___    
(3x − 2)(x + 1)
 
    =     7(x + 1) − 4(x − 1)  
(3x − 2)(x − 1)(x + 1)
 
    =    _ 7x + 7 − 4x + 4_  
(3x − 2)(x − 1)(x + 1)
 
    =   ___ __3x + 11__ ___
(3x − 2)(x − 1)(x + 1)

Example 8.   Symmetrically, if the numerator of a fraction is a sum, then we can rewrite that fraction as a sum of fractions:

a + b + c
      d		 =  a
d		 + b
d		 + c
d		 .

Problem 10.   Rewrite each of the following as a sum of fractions, and simplify.

  a)    1 + 2 + 3
      6		 = 1
6		 + 2
6		 + 3
6		 = 1
6		 + 1
3		 + 1
2
  b)    2n2 − 4n + 1
      n2		 = 2n2
 n2		 − 4n
n2		 +  1 
n2		 = 2 − 4
n		 +  1 
n2
  c)    x³ + 4x2 + 2
       2x5		 =  x³ 
2x5		 + 4x2
2x5		 +  2 
2x5		 =  1 
2x2		 +  2 
x3		 +  1 
x5
  d)    x − 1
x + 1		 =    x   
x + 1		 −    1   
x + 1
  Example 9.   Simplify  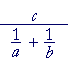  add fractions
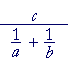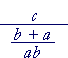  Solution.     add fractions   =   add fractions
 
    =   c ·     ab   
b + a		    (Definition of division)
 
    =     cab  
b + a		   or     abc  
a + b

Problem 11.   Simplify.

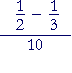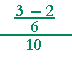  a)   add fractions   =  
add fractions
   =   1
6		  ·   1 
10		   =    1 
60
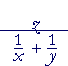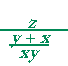  b)   add fractions   =  
add fractions
   =  z ·    xy  
y + x		  =    zxy  
y + x
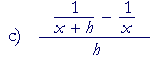add fractions   =   x − (x + h)
  (x + h)x		  ·  1
h
    =   x − x − h
  (x + h)x		  ·  1
h
    =       −h    
(x + h)x		  ·  1
h
    =   −       1     
(x + h)x		 , on canceling the h's.

See Lesson 22, Problem 3h.

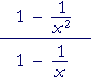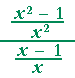  d)    add fractions   =  
add fractions
   =   (x + 1)(x − 1)
         x2		  ·    x  
x − 1		   =   x + 1
   x

Or, on recognizing the numerator as the Difference of Two Squares:

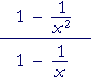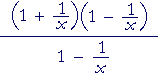  add fractions   =   add fractions   =  1 +  1
x		  =   x + 1
   x
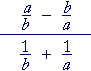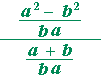 e)    add fractions   =  
add fractions
 
    =   (a + b)(a − b)
        ba		  ·    ba  
a + b
 
    =   a − b
end

Next Lesson:  Equations with fractions

Table of Contents | Home

Please make a donation to keep TheMathPage online.
Even $1 will help.

Copyright © 2021 Lawrence Spector

Questions or comments?

E-mail:  teacher@themathpage.com