15
MULTIPLYING BINOMIALS
Quadratic trinomials
A binomial is a sum of two terms. a + b.
A trinomial is a sum of three terms, while a multinomial is more than three.
An expression in which the highest exponent is 2 --
2x2 − 7x + 5
-- is called a quadratic.
The expression above is called a quadratic trinomial.
Problem 1. Which of the following is a quadratic?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
a) 5x2 − 2x + 4 Yes. 2 is the highest exponent.
| b) | 4x − 9 No. | c) | x3 + x2 + 1 No. | ||||
| d) | y2 + 8y + 10 Yes. | e) | x2 + x5 No. | f) | z2 Yes. | ||
Multiplying binomials
(2x + 3)(x + 5)
Multiplying binomials come up so often that the student should be able to write the product quickly and easily. It is one of the skills of algebra. Therefore, let us multiply those binomials and see what results. First, we will distribute 2x to (x + 5), then we will distribute 3.
| (2x + 3)(x + 5) | = | 2x2 + 10x + 3x + 15 |
| = | 2x2 + 13x + 15. | |
When we multiply two such binomials, then, what form is produced?
A quadratic trinomial.
Now, the first term of the trinomial is no mystery: It is 2x · x. And the last term is no problem either -- it is 3 · 5. And so the only question is: Where does the middle term 13x come from?
The middle term is the sum of the like terms: 10x + 3x :
| (2x + 3)(x + 5) | = | 2x2 + 10x + 3x + 15 |
| = | 2x2 + 13x + 15. | |
If we say that when multiplying binomials, there are four steps --
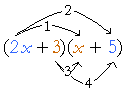
-- then which steps produce the middle term, which is the sum of the like terms?
The 2nd plus the 3rd.
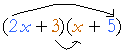
Or as we often call them, the "Outers" plus the "Inners."
It is skillful to be able to pick out the like terms quickly -- to point at them mentally with your eyes. Because symmetrically we will want to factor 2x2 + 13x + 15.
Will it be factored as
(2x + 5)(x + 3) ?
Or as
(2x + 3)(x + 5) ?
The key lies in choosing the one that correctly gives the middle term, 13x.
In the first possibility, can we make 13x by combining the Outers plus the Inners: 6x with 5x ?
No, we cannot. But in the second possibility we can:
10x + 3x = 13x.
2x2 + 13x + 15 will therefore be correctly factored as
(2x + 3)(x + 5).
To check that, the student should practice adding the like terms mentally. That is, to multiply
(2x + 3)(x + 5) ,
look at 2x and x and write 2x2.
Next, look at 2x · 5 and 3 · x together -- "10x + 3x" -- and write 13x.
Finally, 3 · 5 = 15.
(2x + 3)(x + 5) = 2x2 + 13x + 15.
With practice, your eye will get used to picking out the Outers plus the Inners. Those are the like terms. You do algebra with your eyes.
Example 1. (3x − 1)(x + 2). Write only the sum of the like terms.
Answer. 5x. That is,
![]()
6x − x = 5x.
Example 2. Multiply (3x − 1)(x + 2).
Answer. 3x2 + 5x − 2
The first term of the trinomial is 3x · x = 3x2.
The middle term we found to be 5x.
And the third term is −1 · 2 = −2.
Problem 3. Write only the sum of the like terms.
| a) | (2x + 1)(x + 3). 7x | b) | (3x − 2)(x + 4). 10x | |
| c) | (5x − 3)(2x − 1). −11x | d) | (x + 2)(x + 3). 5x | |
| e) | (x + 4)(x − 6). −2x | f) | (x − 5)(x − 3). −8x | |
Problem 4. Write only the trinomial product -- do not write all four terms.
a) (3x + 2)(2x + 1) = 6x2 + 7x + 2
b) (3x + 2)(2x − 1) = 6x2 + x − 2
c) (3x − 2)(2x + 1) = 6x2 − x − 2
d) (3x − 2)(2x − 1) = 6x2 − 7x + 2
Problem 5. Write only the trinomial product.
a) (7x − 2)(5x + 4) = 35x2 + 18x − 8
b) (x − 1)(3x + 8) = 3x2 + 5x − 8
c) (5x − 4)(x − 1) = 5x2 − 9x + 4
d) (2x + 3)(2x + 5) = 4x2 + 16x + 15
e) (6x + 7)(2x − 3) = 12x2 − 4x − 21
f) (4x − 3)(5x − 2) = 20x2 − 23x + 6
Example 3. 1 the coefficient of the x's. (x + 2)(x + 3)
When 1 is the coefficient of each x, the multiplication is especially simple:
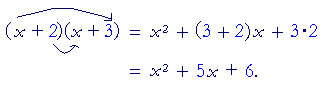
When we add the outers plus the inners, the coefficient of the middle term is the sum of the two numbers. The constant term, as always, is their product.
Example 4. (x − 1)(x + 5) = x2 + 4x − 5.
The outers plus the inners give 4x. More simply, the coefficient of x is −1 + 5. The constant term is −1 · 5.
Problem 6. Write only the trinomial product.
a) (x + 2)(x + 4) = x2 + 6x + 8
b) (x + 2)(x − 4) = x2 − 2x − 8
c) (x − 2)(x − 4) = x2 − 6x + 8
d) (x + 1)(x − 8) = x2 − 7x − 8
e) (x − 1)(x + 8) = x2 + 7x − 8
f) (x − 1)(x − 8) = x2 − 9x + 8
g) (x + 4)(x + 5) = x2 + 9x + 20
h) (x + 2)(x − 8) = x2 − 6x − 16
i) (x − 3)(x − 7) = x2 − 10x + 21
Example 5. Multiply 2(x + 3)(x − 1)
Solution. We can multiply only two factors at a time. First multiply the binomials, then distribute 2:
| 2(x + 3)(x − 1) | = | 2(x2 + 2x − 3) |
| = | 2x2 + 4x − 6. | |
| Example 6. −(x + 4)(x − 5) | = | −(x2 − x − 20) |
| = | −x2 + x + 20. | |
Multiply the binomials. Then remove the parentheses.
Example 7. (x − 4)(x + 5)(x − 2)
Multiply two of the binomials. Then multiply that product with third. (Lesson 14, Example 4.)
| (x − 4)(x + 5)(x − 2) | = | (x − 4)(x2 + 3x − 10) | |
| = | x3 + 3x2 | − 10x | |
| − 4x2 | − 12x + 40 | ||
| = | x3 − x2 | − 22x + 40. | |
Problem 7. Multiply.
a) 4(x − 1)(x + 3) = 4(x2 + 2x − 3) = 4x2 + 8x − 12
b) x(x − 2)(3x + 4) = x(3x2 − 2x − 8) = 3x3 − 2x2 − 8x
c) −(x + 1)(x − 2) = −(x2 − x − 2) = −x2 + x + 2
| d) (x + 1)(x + 2)(x + 3) | = | (x + 1)(x2 + 5x + 6) |
| = | x3 + 5x2 + 6x + x2 + 5x + 6 | |
| = | x3 + 6x2 + 11x + 6 | |
| e) (x − 2)(x + 4)(x − 5) | = | (x − 2)(x2 − x − 20) |
| = | x3 − x2 − 20x − 2x2 + 2x + 40 | |
| = | x3 − 3x2 − 18x + 40 | |
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
