Lesson 25, 2nd Level.
Word problems that lead to
equations with fractions
Example 3. Same time problem: Upstream-Downstream.
First, let us explain the meaning of "upstream" and "downstream."
When a boat travels in the same direction as the current, we say that it is traveling downstream.

Thus if b is the speed of the boat in still water, and c is the speed of the current, then its total speed is
Downstream speed = b + c
When a boat travels against the current, it travels upstream.
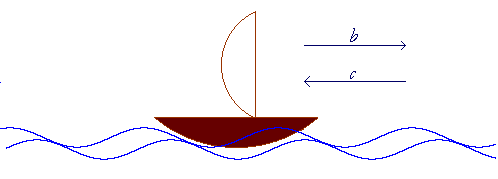
In this case, its total speed is
Upstream speed = b − c
Problem. The speed of a boat in still water is 30 mph. It takes the same time for the boat to travel 5 miles upstream as it does to travel 10 miles downstream. Find the speed of the current.
Solution. The key to this type of problem is same time. That will give the equation,
Time upstream = Time downstream
Now, speed, or velocity, is distance divided by time -- so many miles per hour:
| v | = | d t |
Therefore,
| t | = | d v |
The equation will be
| Time upstream | = | Time downstream | |
| Distance upstream Speed upstream |
= | Distance downstream Speed downstream |
|
| Let x be the speed of the current. Then according to the problem: | |||
| _5_ 30 − x |
= | 10 30 + x |
|
| Therefore, | |||
| 5(30 + x) | = | 10(30 − x) | |
| 150 + 5x | = | 300 − 10x | |
| 5x + 10x | = | 300 − 150 | |
| 15x | = | 150 | |
| x | = | 10 mph | |
Problem 5. The speed of a boat in still water is 15 mi/hr. If the boat travels 8 miles downstream in the same time it takes to travel 4 miles upstream, what is the speed of the current?
To see the equation, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
But do the problem yourself first!
| Time upstream | = | Time downstream | |
|
Distance upstream Speed upstream |
= |
Distance downstream Speed downstream |
|
| Let x be the speed of the current. Then according to the problem: | |||
|
_4_ 15 − x |
= |
8 15 + x |
|
| 4(15 + x) | = | 8(15 − x) | |
| 60 + 4x | = | 120 − 8x | |
| 4x + 8x | = | 120 − 60 | |
| 12x | = | 60 | |
| x | = | 5 mph | |
Problem 6. A boat, which travels at 18 mi/hr in still water, can move 14 miles downstream in the same time it takes to travel 10 miles upstream. Find the speed of the current.
|
Distance upstream Speed upstream |
= |
Distance downstream Speed downstream |
|
|
_10_ 18 − x |
= |
14 18 + x |
|
| 10(18 + x) | = | 14(18 − x) | |
| 180 + 10x | = | 252 − 14x | |
| 10x + 14x | = | 252 − 180 | |
| 24x | = | 72 | |
| x | = | 3 mph | |
Problem 7. Train A has a speed 15 mi/hr greater than train B. If train A travels 150 miles in the same time train B travels 120 miles, what are the speeds of the two trains?
Solution. Let x be the speed of train A. Then the speed of train B is x − 15.
| Train A's time | = | Train B's time | |
|
A's distance A's speed |
= |
B's distance B's speed |
|
|
150 x |
= |
120 x − 15 |
|
| 150(x − 15) | = | 120x | |
| 150x − 150· 15 | = | 120x | |
| 30x | = | 150· 15 | |
| x | = |
150· 15 30 |
|
| = |
150 2 |
||
| x | = | 75 mph | |
| x − 15 | = | 60 mph | |
Problem 8. A train travels 30 mi/hr faster than a car. If the train covers 120 miles in the same time the car covers 80 miles, what is the speed of each of them?
Solution. Let x be the speed of the train. Then the speed of the car is x − 30.
| Train's time | = | Car's time | |
|
Train's distance Train's speed |
= |
Car's distance Car's speed |
|
|
120 x |
= |
80 x − 30 |
|
| 120(x − 30) | = | 80x | |
| 120x − 120· 30 | = | 80x | |
| 40x | = | 120· 30 | |
| x | = |
120· 30 40 |
|
| = | 3· 30 | ||
| x | = | 90 mph | |
| x − 30 | = | 60 mph | |
Example 4. Total time problem. Katrina drove her car to Boston at a speed of 100 kph (kilometers per hour). She drove back at 75 kph. The total driving time was 7 hours. How far away was Boston?
Solution. Let x be the distance to Boston. Then
Time going + Time returning = Total time.
Again, time is
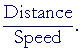 |
|||
| = | 7. | ||
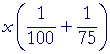 |
= | 7. | x is a common factor. |
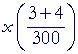 |
= | 7. | Lesson 24 of Arithmetic |
| x | = | Lesson 9, Example 6. | |
| = | 300 km. | ||
Problem 9. You have exactly h hours at your disposal. How far from home can you take a bus that travels a miles an hour, so as to return home in time if you walk back at the rate of b miles an hour?
Solution. Let x = that distance. Then
Time going + Time returning = Total time.
| x a |
+ | x b |
= | h | ||
| bx + ax | = | hab | ||||
| (a + b)x | = | hab | ||||
| x | = | _hab_ a + b |
||||
Example 5. Job problem. Raymond can do a job in 3 hours, while it takes Robert 2 hours. How long will it take them if they work together?
Solution. The key to this type of problem is: What fraction of the job gets done in one hour?
For example, if a job takes 3 hours, then in one hour, ![]() will get done.
will get done.
In general, if a job takes x hours, then in one hour, ![]() will get done.
will get done.
So, let x answer the question. Let x be how long will it take them if they work together. Then ![]() is that fraction of the job that gets done in one hour.
is that fraction of the job that gets done in one hour.
We have,
| 1 x |
= | 1 3 |
+ | 1 2 |
For in one hour, Raymond does ![]() of the job, and Robert,
of the job, and Robert, ![]() .
.
Since x, or its reciprocal, is already isolated on the left, simply add the fractions on the right:
| 1 x |
= | 2 + 3 6 |
= | 5 6 |
Therefore, on taking reciprocals,
| x | = | 6 5 |
= 1 | 1 5 |
hours. | |||
Problem 10. Carlos can do a certain job in three days, while it takes Alec six days. If they work together, how long will it take them?
Let x be that time. Here is the equation:
|
1 x |
= |
1 3 |
+ |
1 6 |
||
| = |
2 + 1 6 |
|||||
| = |
1 2 |
|||||
Therefore,
| x | = | 2 days. | |||
Problem 11. If Jane can do a certain job in 6 hours, but it takes Ana only 4 hours, how long will it take them if they work together?
|
1 x |
= |
1 6 |
+ |
1 4 |
||
| = |
2 + 3 12 |
|||||
|
1 x |
= |
5 12 |
||||
| x | = |
12 5 |
||||
| = | 2 |
2 5 |
hours. |
Problem 12. Two people working together can complete a job in six hours. If one of them works twice as fast as the other, how long would it take the faster one working alone?
Solution. Let x = How long it takes the faster one.
Then the other takes 2x.
Here is the equation:
|
1 6 |
= |
1 x |
+ |
1 2x |
|
| The LCM is 6x. Here is the cleared equation: | |||||
| x | = | 6 + 3 | |||
| = | 9 hours, | ||||
Problem 13. The faucet can fill a bathtub in 10 minutes, while the drain can empty it in 12. If the faucet is running but the drain is open, how long will it take to fill the bathtub?
|
1 x |
= |
1 10 |
− |
1 12 |
||
| = |
6 − 5 60 |
|||||
| = |
1 60 |
|||||
| x | = | 60 minutes. | ||||
Next Lesson: Radicals: Rational and irrational numbers
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com