Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

CONSTRUCTIONS
Book I. Proposition 1
The formal divisions of a proposition
THE LOGICAL THEORY OF PLANE GEOMETRY consists of first principles followed by propositions, of which there are two kinds: theorems and problems. A theorem proposes a statement to prove. A problem proposes a task to accomplish.
Our first proposition is a problem: On a given straight line AB we will be asked to draw an equilateral triangle. It is not difficult.
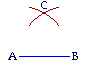
Place the point of the compass at the point A; adjust the compass so that the pencil is at the point B; and draw an arc. Next, with the same compass setting, place the point at B and draw an arc, letting it intersect the first at C. Upon drawing the straight lines CA, CB, the triangle will be equiangular.
In the formal proof below, we must do three things:
1. We must describe the construction.
| 2. | We must then prove that the figure we have constructed is in fact an equilateral triangle; that is, that it satisfies the definition of one. |
| 3. | We must authorize every statement of the construction and the proof by citing a first principle. As we continue, we will authorize those statements by propositions that we have already proved. That is what is called rigor in mathematics. |
This and all the formal proofs are exercises in rhetoric, which is the art of using language as a means of persuasion.
To minimize scrolling, we will repeat the figures.
PROPOSITION 1. PROBLEM
| 1. | On a given straight line to construct an equilateral triangle. | |
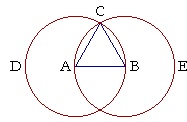
| 2. | Let AB be the given straight line; | |||
| 3. | we are required to construct an equilateral triangle on AB. | |||
| 4. | With A as center and with radius AB, draw the circle BCD; | |||
| (Postulate 3) | ||||
| 5. | with B as center and with radius BA, draw the circle ACE; | |||
| (Postulate 3) | ||||
| 6. | and from the point C, where the circles intersect one another, | |||
| 7. | draw the straight lines CA and CB. | (Postulate 1) | ||
| 8. | Then, since the point A is the center of circle BCD, | ||||||||||||||||||||||
| 9. | AC is equal to AB. | (Definition 16) | |||||||||||||||||||||
| 10. | And since the point B is the center of circle ACE, | ||||||||||||||||||||||
| 11. | BC is equal to AB. | ||||||||||||||||||||||
| 12. | But we have shown that CA is also equal to AB; | ||||||||||||||||||||||
| 13. | therefore CA, CB are each equal to AB. | ||||||||||||||||||||||
| 14. | And things that are equal to the same thing are equal to one another; | ||||||||||||||||||||||
| (Axiom 1) | |||||||||||||||||||||||
| 15. | therefore CA is equal to CB . | ||||||||||||||||||||||
| 16. | Therefore the three straight lines CA, AB, BC are equal to one | ||||||||||||||||||||||
| 17. | another. | ||||||||||||||||||||||
| 18. | Therefore triangle ABC is equilateral, | (Definition 9) | |||||||||||||||||||||
| 19. | and we have constructed it on the given straight line AB. | ||||||||||||||||||||||
| 20. | Which is what we were required to do. | ||||||||||||||||||||||
![]()
This first proposition shows not only how to draw an equlateral triangle. It proves that since we can construct one, then equilateral triangles exist logically. See the Commentary on the Definitions.
The following is a guide to the rhetoric.
The formal divisions of a proposition
The general statement of a proposition is called its enunciation. The enunciation of this proposition appears in italics in line 1. It states what is given and what we must conclude or do.
Following the enunciation is the setting-out, line 2. Here, we apply what is given to a specific figure. Following that is the specification, line 3. Here, with regard to that figure we state specifically what we are required to prove or do.
Next comes the construction itself (lines 4 through 7), and following that is the proof (lines 8 through 17).
Finally, we have the closing. In the closing we refer back to the enunciation and we confirm what we have done or shown. Lines 18 through 20 are the closing.
A problem traditionally closed with the Latin Quod erat faciendum, literally, Which was to be done, abbreviated Q.E.F. A theorem closed with Quod erat demonstrandum, Which was to be proved, abbreviated Q.E.D. We will begin to use those closings shortly.
These are the six formal divisions of a proposition. The stability they have had for over 2500 years comes from the aesthetics of clear demonstration, which belongs to the study of rhetoric. ("Tell them what you're going to do; do it; tell them that you've done it.")
The citations of Postulates, Definitions, and Axioms that we have placed on the extreme right, were not included in the Elements. It has become the custom however to include them as a guide to the reasoning. We hope they will not distract from the elegance of Euclid's demonstrations; a balance which is upset with today's two-column proofs.
Tacit assumptions
Were all parts of the proposition clear to you? If not, then once you do understand, you might find your own way, a clearer way, to express it.
Was the demonstration convincing? That is, were the arguments valid, and were they based only on things that were previously acknowledged? For, every statement we make must belong to some logical category. It must be a Definition, a Postulate, an Axiom, or a proposition that we have already established. That is called the axiomatic method.
Or were there some tacit assumptions? (The word tacit means not spoken; and so a tacit assumption is one that is not explicitly stated. For example, if a is greater than b, and b is greater than c, then a tacit assumption might be that a is greater than c.)
Were there any tacit assumptions? What about the inference that the two circles actually do intersect one another are the point called C? (Line 6.) Does any postulate or axiom guarantee that? If not, can you suggest a postulate that would?
(Such a postulate would have to state something extremely obvious, and therefore might be all the more difficult to articulate. It would have to imply that when a continuous line exists on both sides of another line, then at some point it must cross that other line.)
In a rigorous treatment of any logical science, an attempt is made to expose all tacit assumptions. This means that every proof is submitted to a searching analysis. We shall not do this. We have brought up the issue of tacit assumptions this once, and we shall leave it at that -- which need not prevent the student from questioning.
Thus mathematics is not a static subject, for there will always be individuals who are dissatisfied with current methods, conceptions, and proofs. Only by calling into question what is "obvious" or what is approved, can science ever penetrate to what is true.
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com