Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

THE THEORY OF PARALLEL LINES
Book I. PROPOSITIONS 29, 30, and POSTULATE 5
Postulate 5 versus Playfair's Axiom
HERE AGAIN is Proposition 27.
If a straight line that meets two straight lines makes the alternate angles equal, then the two straight lines are parallel.
We are about to prove Proposition 29, which is its converse:
If two straight lines are parallel, then a straight line that meets them makes the alternate angles equal.
To prove that the alternate angles are equal, we must have a sufficient condition for their being equal. But this proposition is the condition. Therefore we will have to prove this proposition indirectly. Now, a sufficient condition for the alternate angles not being equal is the following partial inverse to Proposition 28:
If a straight line that meets two straight lines makes the interior angles on the same side less than two right angles, then those two straight lines, if extended, will meet on that same side.
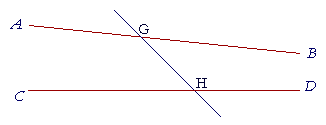
That is, if the angles BGH, GHD are not equal to two right angles, then the straight lines AB, CD are not parallel.
The question is: Is it possible to prove that from the existing first principles?
The answer, the student may be surprised to learn, is no. Mathematicians tried for over two thousand years. But from the existing first principles, no one could. It is in fact Euclid's famous, and controversial, Postulate 5.
Here then is Proposition 29. It is the converse of Proposition 27 and Proposition 28 combined. The indirect proof assumes that the alternate angles are not equal. It will then turn out the straight lines are not parallel -- which by hypothesis they are! The proof will require Postulate 5.
PROPOSITION 29. THEOREM
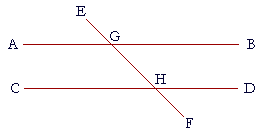
| If two straight lines are parallel, then a straight line that meets them makes the alternate angles equal, it makes the exterior angle equal to the opposite interior angle on the same side, and it makes the interior angles on the same side equal to two right angles. | |
| Let the straight lines AB, CD be parallel, and let the straight line EF meet them; then it makes the alternate angles AGH, GHD equal; it makes the exterior angle EGB equal to the opposite interior angle GHD; and it makes the interior angles on the same side, angles BGH, GHD, equal to two right angles. |
|
 |
|
| (We will prove only up to "makes the alternate angles equal." The rest will be left to the student. Problem 4.) | |
| For, if angle AGH is not equal to angle GHD, then one of them is greater. | |
| Let angle AGH be greater than angle GHD; | |
| and to each of them join angle BGH; | |
| then angles BGH, AGH are greater than angles BGH, GHD. | |
| But angles BGH, AGH are together equal to two right angles; | (I. 13) |
| therefore angles BGH, GHD are together less than two right angles. | |
| But straight lines if extended from angles less than two right angles, will meet. | (Postulate 5) |
| Therefore AB, CD, if extended, will meet. | |
| But they do not meet because by hypothesis they are parallel. | |
| Therefore angle AGH is not unequal to angle GHD; | |
| it is equal to it. | |
| Therefore, if two straight lines etc. Q.E.D. | |
Postulate 5 versus Playfair's Axiom
In his Notes on the Elements, Todhunter observes,
The theory of parallel straight lines has always been considered the great difficulty of elementary geometry, and many attempts have been made to overcome the difficulty in a better way than Euclid had done.
(Elibron Classics, page 262.) He is referring of course to the fifth Postulate. Nevertheless, he continues,
. . . after the axiom is once admitted, the remaining process is simple and clear.
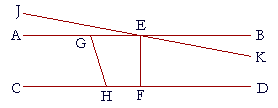
We can gain some insight into Postulate 5 in this figure. The straight line EF is perpendicular to both AB and CD -- angles BEF, EFD are two right angles. And we can see that AB, CD are therefore parallel.
But if GH is any straight line that meets AB, CD, and angles EGH, GHF are together equal to two right angles, then again AB, CD are parallel. (I-28)
Finally, if, when EF meets JK and CD, it makes the interior angles on the same side less than two right angles, then JK, CD are not parallel, and they will meet on that same side.
That is Postulate 5.
Some writers however have replaced Postulate 5 with the following, which they think is intuitively simpler:
Two intersecting straight lines cannot both be parallel to a third line.
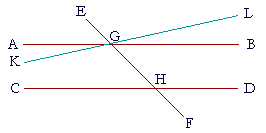
That is, through the point G it is impossible that both AB and KL are parallel to CD.
The student should not be fooled by the word games of the non-Euclidean geometries, which also contain the term "straight line." They are non-Euclidean because the surface in question is not a plane.
The proposition above has been called Playfair's Axiom, after the 18th century English mathematician John Playfair. If we grant it in place of Postulate 5, then, in Propostion 29 we would again assume that the alternate angles AGH, GHD are not equal. We would continue:
Draw a straight line KL through G that makes angle KGH equal to angle GHD.

Then, since those alternate angles are equal, KL is parallel to CD.
(I. 27)
Therefore the two straight lines KL, AB that intersect at G are both parallel to CD,
which is impossible. (Playfair's Axiom)
Therefore, angles AGH, GHD are not unequal; they are equal. Q.E.D.
Now, upon granting Playfair's Axiom, it is possible to prove Postulate 5 as a theorem. And conversely, if we grant Postulate 5, then we can prove Playfair's Axiom. (Problem 5.) The choice of which propositions to take as the postulates and which to take as the theorems is simply that: a matter of choice. Ultimately, the choice is aesthetic. The postulates typically are those which appear most elementary, or which make the least strain on the intellect, or which in some way are immediately satisfying. (These are aesthetic choices, because a postulate must appear that way to someone.) Thus, as Heath points out (Dover, page 313), Playfair asks us to assume what is impossibile, namely that two intersecting lines cannot both be parallel to a third, while Euclid asserts what is possible, namely that two straight lines under certain conditions will meet.
The two postulates nevertheless are equivalent to one another, in the sense that we can deduce each one from the other. We see therefore that there is no unique set of postulates from which to deduce the remainder of a theory. Hence there is never a unique reason why we say that a theorem is true.
For, the theorems are true whether we prove them or not. They are not true because we prove them. We prove them because they are true.
![]()
PROPOSITION 30. THEOREM
| Straight lines that are parallel to the same straight line are parallel to one another. |
We leave the rest to the student. (Problem 7)
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com