15
EVALUATING e
IN THE previous lesson, we saw the following definition of e:
![]()
| On changing the variable from x to | 1 n |
, we have: |
| e | = | 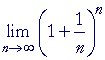 |
| By letting n take on larger and larger values in | 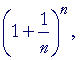 |
we can come |
closer and closer to a decimal value for e.
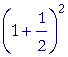 |
= 2.25 |
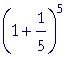 |
= 2.489 |
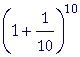 |
= 2.594 |
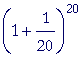 |
= 2.6534 |
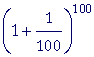 |
= 2.705 |
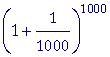 |
= 2.7169 |
2.7169 is an approximate value for e.
As a more efficient approach, we can derive a sequence that converges to e more rapidly.
| To | 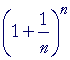 |
let us apply the binomial theorem: |
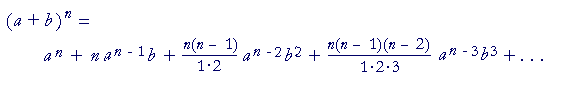
| On putting a = 1 and b = | 1 n |
, we get |

Now, e is the limit of that sum as n becomes infinite. When that happens, each fraction that depends on n approaches 1 because 1 is the quotient of the leading coefficients. (Lesson 4.)
Therefore, on taking the limit of that sum as n becomes infinite:
![]()
Notice: Each term can be derived from the previous term. The second term follows from the first by dividing it by 1. The next term follows by dividing by 2. The next term, by dividing by 3. The next, by 4. And so on. e is the limit of the sequence of partial sums. Here is the sum of the first 10 terms expressed as decimals:
| 11st term | 1.000000 | ||
| 12nd term | (dividing by 1) | 1.000000 | |
| 13rd term | (dividing by 2) | 0.500000 | |
| 14th term | (dividing by 3) | 0.166667 | |
| 15th term | (dividing by 4) | 0.041667 | |
| 16th term | (dividing by 5) | 0.008333 | |
| 17th term | (dividing by 6) | 0.001389 | |
| 18th term | (dividing by 7) | 0.000198 | |
| 19th term | (dividing by 8) | 0.000025 | |
| 10th term | (dividing by 9) | 0.000003 | |
| Sum | 2.718282 | ||
And so after only 10 terms, we obtain a value of e accurate to 6 decimal digits. That is an example of a rapidly converging series.
e however, like π, is an irrational number.
Problem. In this term of the binomial theorem,
![]() an − 2b2
an − 2b2
| show that, on putting a = 1 and b = | 1 n |
, the term becomes |
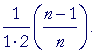
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
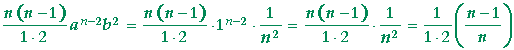
![]()

Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
