13
ROOTS OF POLYNOMIALS
OF DEGREE GREATER THAN 2
The fundamental theorem of algebra
Proof of the integer root theorem
IN THIS TOPIC we will see how to find the roots of a polynomial of degree greater than 2. This will depend on the previous topic: Synthetic division.
We saw in that topic what is called the factor theorem.
The Factor Theorem. x − r is a factor of a polynomial P(x) if and only if r is a root of P(x).
This means that if a polynomial can be factored, for example, as follows:
P(x) = (x − 1)(x + 2)(x + 3)
then the theorem tells us that the roots are 1, −2, and −3.
Conversely, if we know that roots of a polynomial are −2, 1, and 5, then the polynomial has the following factors:
(x + 2)(x − 1)(x − 5).
We could then multiply out and know the polynomial that has those three roots.
We will see below how to prove the factor theorem .
a) Use the Factor Theorem to prove: (x + 1) is a factor of x5 + 1.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
−1 is a root of x5 + 1. For, (−1)5 + 1 = −1 + 1 = 0.
Therefore, according to the Factor Theorem,
[x −(−1)] = (x + 1) is a factor.
b) Use synthetic division to find the other factor.
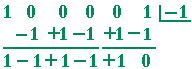
Therefore, x5 + 1 = (x + 1)(x4 − x3 + x2 − x + 1)
Following this same procedure, we could prove:
(x + a) is a factor of x5 + a5,
and completely generally:
(x + a) is a factor of xn + an, where n is odd.
The Fundamental Theorem of Algebra
The following is called the Fundamental Theorem of Algebra:
A polynomial of degree n has at least one root, real or complex.
This apparently simple statement allows us to conclude:
A polynomial P(x) of degree n has exactly n roots, real or complex.
If the leading coefficient of P(x) is 1, then the Factor Theorem allows us to conclude:
P(x) = (x − rn)(x − rn − 1). . . (x − r2)(x − r1)
Hence a polynomial of the third degree, for example, will have three roots. And if they are all real, then its graph will look something like this:
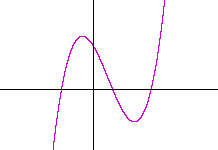
For, the three roots are the three x-intercepts.
Note: If we imagine that the graph begins to the left of the y-axis, then this graph begins below the x-axis. Why? Because in any polynomial, the leading term eventually will dominate. If the leading term is positive and the polynomial is of odd degree, then when x is a large negative number -- that is, far to the left of the origin -- then an odd power of a negative number is itself negative. The graph will be below the x-axis.
As for a polynomial of the fourth degree, it will have four roots. And if they are all real, then its graph will look something like this:
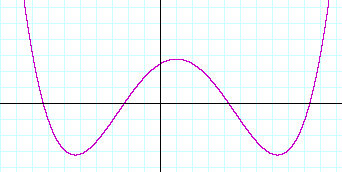
Here, the graph on the far left is above the x-axis. For when the polynomial is of even degree (and the leading coefficient is positive), then an even power of a negative number will be positive. The graph will be above the x-axis.
Example 1. Write the polynomial with integer coefficients that has the following roots: −1, ¾.
Solution. Since −1 is a root, then (x + 1) is a factor. As for the root ¾, we would have the solution
| x | = | 3 4 |
| which implies | ||
| 4x | = | 3 |
| 4x − 3 | = | 0 |
The factors are (4x − 3)(x + 1).
The polynomial is 4x2 + x − 3.
Problem 2. Determine the polynomial whose roots are −1, 1, 2, and sketch its graph.
The factors are (x + 1)(x − 1)(x − 2). On multiplying out, the polynomial is (x2 − 1)(x − 2) =
x3 − 2x2 − x + 2.
Here is the graph:
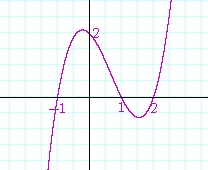
The y-intercept is the constant term 2. In every polynomial the y-intercept is the constant term because the constant term is the value of y when x = 0.
Problem 3. Determine the polynomial with integer coefficients whose roots are −½, −2, −2, and sketch the graph.
The factors are (2x + 1)(x + 2)2. On multiplying out, the polynomial is (2x + 1)(x2 + 4x + 4) =
2x3 + 9x2 + 12x + 4.
Here is the graph:
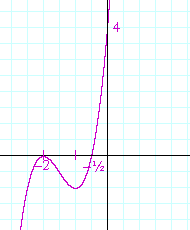
−2 is a double root. The graph does not cross the x-axis.
Question. If r is a root of a polynomial p(x), then upon dividing p(x) by x − r, what remainder should you expect?
0. Since r is a root, then x − r is a factor of p(x).
Problem 4. Is x = 2 a root of this polynomial:
x6 − 3x5 + 3x4 − 3x3 + 3x2 −3x + 2 ?
Use synthetic division to divide the polynomial by x − 2, and look at the remainder.
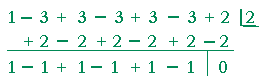
The remainder is 0. 2 is a root of the polynomial.
Example 2. Find the three roots of
P(x) = x3 − 2x2 − 9x + 18,
given that one root is 3.
Solution. Since 3 is a root of P(x), then according to the factor theorem, x − 3 is a factor. Therefore, on dividing P(x) by x − 3, we can find the other, quadratic factor.
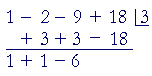
We have
| x3 − 2x2 − 9x + 18 | = | (x2 + x − 6)(x − 3) |
| = | (x − 2)(x + 3)(x − 3) | |
The three roots are: 2, −3, 3.
Again, since x − 3 is a factor of P(x), the remainder is 0.
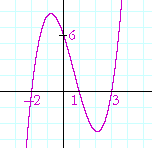
Problem 5. Sketch the graph of this polynomial,
y = x3 − 2x2 − 5x + 6,
given that one root is −2.
Since −2 is a root, then (x + 2) is a factor. To find the other, quadratic factor, divide the polynomial by x + 2. Note that the root −2 goes in the box:
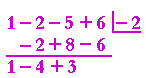
We have
| x3 − 2x2 − 5x + 6 | = | (x2 − 4x + 3)(x + 2) |
| = | (x − 1)(x − 3)(x + 2) | |
The three roots are: 1, 3, −2. Here is the graph:
A strategy for finding roots
What, then, is a strategy for finding the roots of a polynomial of degree n > 2?
We must be given, or we must guess, a root r. We can then divide the polynomial by x − r, and hence produce a factor of the polynomial that will be one degree less. If we can discover a root of that factor, we can continue the process, reducing the degree each time, until we reach a quadratic, which we can always solve.
Here is a theorem that will help us guess a root.
The integer root theorem. If an integer is a root of a polynomial whose coefficients are integers and whose leading coefficient is ±1, then that integer is a factor of the constant term.
We will prove this below.
This Integer Root Theorem is an instance of the more general Rational Root Theorem:
If the rational number r/s is a root of a polynomial whose coefficients are integers, then the integer r is a factor of the constant term, and the integer s is a factor of the leading coefficient.
Example 3. What are the possible integer roots of x3 − 4x2 + 2x + 4?
Answer. If there are integer roots, they will be factors of the constant term 4; namely: ±1, ±2, ±4.
Now, is 1 a root? To answer, we will divide the polynomial by x − 1, and hope for remainder 0.
| 1 | − 4 | + 2 | + 4 | |1 |
| + 1 | − 3 | − 1 | ||
| ------------------------------------------------------------------------------------------------------- | ||||
| 1 | − 3 | − 1 | + 3 | |
The remainder is not 0. 1 is not a root. Let's try −1:
| 1 | − 4 | + 2 | + 4 | |−1 |
| − 1 | + 5 | − 7 | ||
| ------------------------------------------------------------------------------------------------------ | ||||
| 1 | − 5 | + 7 | − 3 | |
The remainder again is not 0. Let's try 2:
| 1 | − 4 | + 2 | + 4 | |2 |
| + 2 | − 4 | − 4 | ||
| ------------------------------------------------------------------------------------------------------- | ||||
| 1 | − 2 | − 2 | + 0 | |
Yes! 2 is a root. We have
x3 − 4x2 + 2x + 4 = (x2 − 2x − 2)(x − 2)
We can now find the roots of the quadratic by completing the square. As we found in Topic 11:
x = 1 ± ![]()
Therefore, the three roots are:
1 + ![]() , 1 −
, 1 − ![]() , 2.
, 2.
Problem 6.
a) What are the possible integer roots of this polynomial?
x3 − 2x2 − 3x + 1
±1. They are the only factors of the constant term.
b) Does that polynomial have integer roots?
No, because neither 1 nor −1 will make that polynomial equal to 0. Synthetic division by both ±1 does not give remainder 0.
Problem 7. Factor this polynomial into a product of linear factors.
x3 + 2x2 − 5x − 6
We must find the roots. The possible integer roots are ±1, ±2, ±3, ±6. Synthetic division reveals that −1 is a root.
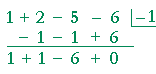
Therefore,
| x3 + 2x2 − 5x − 6 | = | (x + 1)(x2 + x − 6) |
| = | (x + 1)(x + 3)(x −2) | |
Conjugate pairs
If the irrational number a + ![]() is a root, then its conjugate a −
is a root, then its conjugate a − ![]() is also a root. (See Skill in Algebra, Lesson 28.) And if the complex number a + bi is a root, then so is its conjugate, a − bi.
is also a root. (See Skill in Algebra, Lesson 28.) And if the complex number a + bi is a root, then so is its conjugate, a − bi.
Example 4. A polynomial P(x) has the following roots:
−2, 1 + ![]() , 5i.
, 5i.
What is the smallest degree that P(x) could have?
Answer. 5. For, since 1 + ![]() is a root, then so is its conjugate, 1 −
is a root, then so is its conjugate, 1 − ![]() . And since 5i is a root, so is its conjugate, −5i.
. And since 5i is a root, so is its conjugate, −5i.
P(x) has at least these 5 roots:
−2, 1 ± ![]() , ±5i.
, ±5i.
Problem 8. Construct a polynomial that has the following root:
a) 2 + ![]()
Since 2 + ![]() is a root, then so is 2 −
is a root, then so is 2 − ![]() . Therefore, according to the theorem of the sum and product of the roots, they are the roots of x2 − 4x + 1.
. Therefore, according to the theorem of the sum and product of the roots, they are the roots of x2 − 4x + 1.
b) 2 − 3i
Since 2 − 3i is a root, then so is 2 + 3i. Again, according to the theorem of the sum and product of the roots, they are the roots of x2 − 4x + 13.
See Topic 10, Example 7.
Problem 9. Construct a polynomial whose roots are 1 and 5i.
Since 5i is a root, then so is its conjugate, −5i. They will be the roots of a quadratic factor of the polynomial. The sum of those roots is 0. The product is 25. Therefore the quadratic factor is (x2 + 25).
Next, since 1 is a root, then (x − 1) is a factor. Therefore the polynomial is
(x − 1)(x2 + 25) = x3 − x2 + 25x − 25.
Problem 10. Let f(x) = x5 + x4 + x3 + x2 − 12x − 12. One root is ![]() and another is −2i.
and another is −2i.
If f(x) has integer roots, how many could it have?
One. This is a polynomial of the 5th degree, and has 5 roots. Two are ![]() and −
and −![]() . And two are 2i and −2i.
. And two are 2i and −2i.
Problem 11. Is it possible for a polynomial of the 5th degree to have 2 real roots and 3 imaginary roots?
No, it is not. Since imaginary roots always come in pairs, then if there are any imaginary roots, there will always be an even number of them.
Consider the graph of a 5th degree polynomial with positive leading term. When x is a large negative number, the graph is below the x-axis. When x is a large positive number, it is above the x-axis. Therefore, the graph must cross the x-axis at least once. Now, can you draw the graph so that it crosses the x-axis exactly twice? No, you cannot. A polynomial of odd degree must have an odd number of real roots.
Proof of the factor theorem
x − r is a factor of a polynomial P(x)
if and only if
r is a root of P(x).
First, if (x − r) is a factor of P(x), then P(r) will have the factor (r − r), which is 0. This will make P(r) = 0. This means that r is a root.
Conversely, if r is a root of P(x), then P(r) = 0. But according to the remainder theorem, P(r) = 0 means that upon dividing P(x) by x − r, the remainder is 0. x − r, therefore, is a factor of P(x).
This is what we wanted to prove.
Proof of the integer root theorem
If an integer is a root of a polynomial whose coefficients are integers and whose leading coefficient is ±1, then that integer is a factor of the constant term.
Let the integer r be a root of this polynomial:
P(x) = ±xn + an−1xn−1 + an−2xn−2 + . . . + a2x2 + a1x + a0,
where the a's are integers. Then, since r is a root,
P(r) = ±rn + an−1rn−1 + an−2rn−2 + . . . + a2r2 + a1r + a0 = 0.
Transpose the constant term a0, and factor r from the remaining terms:
r(±rn−1 + an−1rn−2 + . . . + a2r + a1) = −a0
Now the a's are all integers; therefore the expression in parentheses is an integer, which, for convenience, we will call −q:
r(−q) = −a0,
or,
rq = a0.
Thus, the constant term a0 can be factored as rq, if r and q are both integers. Under those conditions, then, r is a factor of the constant term.
This is what we wanted to prove.
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
