2
RATIONAL AND IRRATIONAL
NUMBERS
A proof that square root of 2 is not rational
Which natural numbers have rational square roots?
The decimal representation of irrationals
CALCULUS IS A THEORY OF MEASUREMENT. The necessary numbers are the rationals and irrationals. But let us start at the beginning.
The following numbers of arithmetic are the counting-numbers or, as they are called, the natural numbers:
1, 2, 3, 4, and so on.
(At any rate, those are their symbols, the Arabic numerals.)
If we include 0, we have the whole numbers:
0, 1, 2, 3, and so on.
And upon including their algebraic negatives, we have the integers:
0, ±1, ±2, ±3, and so on.
± ("plus or minus") is called the double sign.
The following are the square numbers, or the perfect squares:
1 4 9 16 25 36 49 64, and so on.
And these are their roots:
1 2 3 4 5 6 7 8, and so on.
The student is no doubt familiar with the radical sign: 
.
= 5.
"The square root of 25 is 5."
Since it is with those symbols—1, 2, 3, 4—that we do written calculations, it has become common to call the symbols themselves "numbers." But a number is more than a symbol. (@ is a symbol; it is not a number.) The number is that to which the symbol refers.
Rational and irrational numbers
1. What is a rational number?
A rational number is simply a number of arithmetic: a whole number, a fraction, a mixed number, or a decimal. They are the numbers with whose names and symbols we count and measure.
Their negative images nowadays are also called rational.
2. Which of the following numbers are rational?
| 1 | −1 | 0 | 2 3 |
− | 2 3 |
5½ | −5½ | 6.085 | −6.085 | 3.1415926535897 |
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
All of them. All decimals are rational. That long one is an approximation to π, which, as we shall see, is not equal to any decimal. For if it were, it would be rational.
3. Why the name rational?
The natural numbers of arithmetic have a ratio to one another. Every number of arithmetic can be written as a fraction, which has the same ratio to 1 as the numerator has to the denominator.
| a b |
: 1 = | a : b. |
A number that has the same ratio to 1 as two natural numbers we say is rational.
Every number of arithmetic proceeds from 1, which is the source. The natural numbers are its multiples, the fractions are its parts. Every number thus has a relationship to 1, which we can always name. ("The number we write as 5 is five times 1." "The number we write as ¾ is three fourths of 1.) Language, we will see, cannot express the relationship of an irrational number to 1.
Upon extending these to the negative numbers of algebra:
4. A rational number can always be written in what form?
| As a fraction | a b |
, where a and b are integers (b  0). |
That is the formal definition of a rational number. That is how a rational number can be made to look.
Finally, we can in principle (by Euclid VI, 9) place any rational number exactly on the number line.
We can say that we truly know a rational number.
*
We will now see that the square root of a number that is not a perfect square—√2, √3, √48—is not a rational number. It is not a number of arithmetic.
Consider √2 ("Square root of 2"). 
is close because
| 7 5 |
· | 7 5 |
= | 49 25 |
—which is almost 2.
To see that there is no rational number whose square is 2, suppose there were. Obviously, it is not a whole number. It will be in the form of a fraction in lowest terms. But the square of a fraction in lowest terms is also in lowest terms.
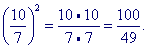
No new factors are introduced and the denominator will never divide into the numerator to give 2—or any whole number.
There is no rational number whose square is 2 or any number that is not a perfect square. We say therefore that 
is an irrational number.
5. Which natural numbers have rational square roots?
Only the square roots of the square numbers; that is, the square roots of the perfect squares.
= 1 Rational
Irrational
Irrational
= 2 Rational
, 
, 
, 
Irrational
= 3 Rational
And so on.
This follows from the same proof that is irrational.
*
An irrational number and 1 are incommensurable. What does that mean?
Every fraction -- every number of arithmetic -- is a sum of unit fractions. And 1 can be written as a multiple of any unit fraction. Every number of arithmetic and 1 will thus be a multiple of the same unit fraction.
For example,
| 3 5 |
= 3 × | 1 5 |
= | 1 5 |
+ | 1 5 |
+ | 1 5 |
. |
| 1 | = 5 × | 1 5 |
= | 1 5 |
+ | 1 5 |
+ | 1 5 |
+ | 1 5 |
+ | 1 5 |
. |
We say in geometry that 
is a common measure of 
and 1. It measures three times and 1 five times.
When two numbers or two lengths have a common measure, then each will be a multiple of the common measure. They will be to one another as two natural numbers.
| 3 5 |
: 1 = | 3 : 5. |
Now an irrational number is not a multiple of any unit fraction. It is not a number of fifths, or tenths, or thousandths, or trillionths. For if it were, it would be rational. An irrational number thus has no common measure with any rational number. Specifically, it has no common measure with 1. We say that they are incommensurable.
Every rational number has a common measure with 1. Incommensurability with 1 is what characterizes an irrational number. We cannot say how an irrational number and 1 are related.
Pythagoras effectively knew that in the 6th century B.C.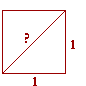 
He realized that the relationship of the diagonal of a square to the side was not as two natural numbers. Their relationship, he said, was without a name.
To say that the diagonal and side of a square are not as two natural numbers, is to say that they are incommensurable.
(Knowledge of a square figure, however, is still rational: The square drawn on the diagonal is twice the square on the side.)
Irrational numbers have been called surds, after the Latin surdus, deaf or mute. Why deaf or mute? Because there is nothing we can hear. An irrational number cannot say how much it is, nor how it is related to 1.
For the earliest use of the terms rational and irrational, see here.
The decimal representation of irrationals
A number is not inherently a decimal. However, when we express a rational number as a decimal, then either the decimal will be exact, as 
= .25, or it will not be, as 
≅ .33333; nevertheless, there will be a predictable pattern of digits. But when we express an irrational number as a decimal, then clearly it will not be exact, because if it were, the number would be rational.
Moreover, there will not be a predictable pattern of digits. For example,
≅ 1.4142135623730950488016887242097
(This symbol ≅ means "is approximately equal to.")
Now, with rational numbers, you sometimes see
= .090909. . .
By writing the equal sign = and three dots (ellipsis) rather than ≅, we mean:
"It is not possible to express exactly as a decimal. However, we can approximate it with as many decimal digits as we please according to the indicated pattern; and the more decimal digits we write, the closer we will be to ."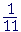
We say that any decimal for is inexact. But the decimal for , which is .25, is exact.
The decimal for an irrational number is always inexact. If we write ellipsis—
= 1.41421356237. . .
—we mean: "No decimal for will be exact. We could continue its rational approximation for as many decimal digits as we please by means of the algorithm, or method, for calculating each next digit (not the subject of these Topics); and again, the more digits we calculate, the closer we will be to ."
We often hear that the decimal goes on forever. Obviously, we cannot produce such a sequence of digits nor could we be aware of one. It is nothing but a thought.
What would it even mean to say that a decimal that never ends "exists"? It certainly does not exist in this world. In quantum mechanics, it is not logical to say that even an electron exists until it is observed.
We are taught of course that certain decimals go on forever, and so we think that's mathematics—that's the way things are. We do not realize that it is a man made conceit.
This writer asserts that what we can actually bring into this world—1.41421356237—has more being for mathematics than what is only a thought.
As for the phrase "goes on forever," we may take it to mean what "infinite" has historically meant in mathematics: There is no limit to the number of digits that we could calculate.
To sum up, a rational number is a number we can name and know exactly, either as a whole number, a fraction, or a mixed number, but not always exactly as a decimal. An irrational number we can never know exactly in any form. No decimal that you or anyone will ever see is equal to , or π, or any irrational number. We know an irrational number only as a rational approximation. That approximation, moreover, is the only relationship of an irrational number to 1.
6. What is a real number?
A real number is what we call any rational or irrational number. They are the numbers we expect to find on the number line. The real numbers are the subject of calculus and of scientific measurement.
The term real number was coined by René Descartes in 1637. It was to distinguish it from an imaginary or complex number
(An actual measurement can result only in a rational number.
An irrational number is required logically or is the result of a definition. Logically, one is necessary upon applying the Pythagorean theorem or as the solution to an equation, such as
x3 = 5. The irrational number π results upon being defined as the ratio of the circumference of a circle to the diameter.)
Problem 1. We have categorized numbers as real, rational, irrational, and integer. Name all the categories to which each of the following belongs.
| a) 3 Real, rational, integer. | b) −3 Real, rational, integer. | |
| c)−½ Real, rational. | d);  Real, irrational. |
|
| e) 5¾ Real, rational. | f) − 11/2 Real, rational. | |
| g) 1.732 Real, rational. | h) 6.920920920. . . Real, rational. | |
| i) 6.92057263. . . Real. And let us assume that it is irrational, that is, no matter how many digits we calculate, they do not repeat. We must assume, therefore, that there is a procedure—a rule—for computing each next digit. For if there were not, then we would not know that symbol's position with respect to order. We would not be able to decide whether it is less than or greater than 6.920572635. Which is to say, it would not be a number. | ||
| (See Are the real numbers really numbers?) | ||
| j) 6.92057263 Real, rational. Every exact decimal is rational. | ||
8. What is a real variable?
A variable is a symbol that takes on values. A value is a number.
A real variable takes on values that are real numbers.
Calculus is the study of functions of a real variable.
Problem 2. Let x be a real variable, and let 3 < x < 4. Name five values that x might have.
*
See The Evolution of the Real Numbers starting with the natural numbers.
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com