22
SIGMA NOTATION FOR SUMS
The sum of consecutive numbers
THIS —Σ—is the Greek letter sigma. We use it to indicate a sum.
For example:
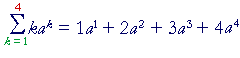
This means that we are to repeatedly add kak. The first time we write it, we put k = 1. That is indicated by the lower index of Σ. The next time, we put k = 2, then 3, and so on, until we come to the upper index, which in this case is 4.
In other words, we are to repeatedly add kak, which we call the argument of the sum, or the summand, starting with k = 1 and ending with k = 4.
k is called a dummy index because it does not actually affect the sum, and we could indicate that sum using any letter we please; for example j:
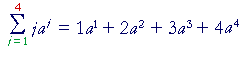
Problem 1. Write the following sums.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | 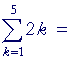 |
2· 1 + 2· 2 + 2· 3 + 2· 4 + 2· 5 |
| = | 2 + 4 + 6 + 8 + 10. |
| b) | 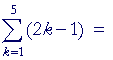 |
1 + 3 + 5 + 7 + 9. |
Example 1. Upper index n.
| = | 1 + 2 + 3 + . . . + (n − 1) + n. |
That is how to use sigma notation to indicate the sum of n consecutive whole numbers. The last term of the sum is n. We indicate the next to last as (n − 1).
Problem 2. Write the following sum.
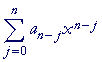 |
= |
Here, the sum begins with j = 0. That is how with sigma notation we indicate a polynomial in x of degree n. (Topic 6, Problem 6.)
| Example 2. | 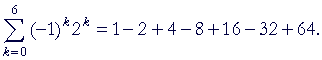 |
When the signs alternate, positive and negative in that way, we call that an alternating series. What causes the signs to alternate is (−1)k. For when k is 0 or an even number, then (−1)k will be +1. But when k is odd, (−1)k will be negative.
See Lesson 13 of Algebra, Example 1 and Problem 7.
Problem 3. Write the following sum.
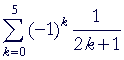 |
= |
Example 3. Use sigma notation to indicate this sum:
2 + 4 + 6 + 8 + . . . + 100.
| Solution. |
2k indicates an even number, which is a multiple of 2. To ensure that 2 is the first term, the lower index is clearly 1. As for the upper index, we can decide that it must be 50 because we must have 2k = 100. Upon solving that equation, k = 50.
Problem 4. Use sigma notation to indicate these sums.
| a) 1 + 3 + 5 + 7 + . . . + 79 = | 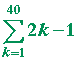 |
| b) 1 − 2 + 3 − 4 + 5 − . . . + 21 = | 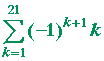 |
| c) 1 + a + a2 + a3 + . . . + an = | 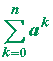 |
Three theorems
| 1. | 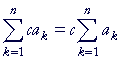 |
A factor that does not depend on the index k
may pass through the summation sign.
| Proof. | 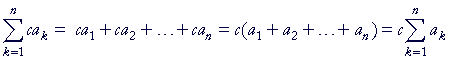 |
| 2. | 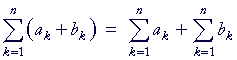 |
A sum that consists of terms may be split into a sum over each term.
Proof.
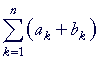 |
= | a1 + b1 + a2 + b2 + . . . + an + bn |
| = | a1 + a2 + . . . + an + b1 + b2 + . . . + bn | |
| = | 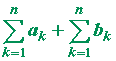 |
|
| 3. | 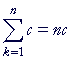 |
If the argument of the summation is a constant, that is, does not depend on the index k,
then the sum is equal to the number of terms times that constant.
| Proof. | 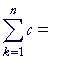 |
c + c + c + . . . + c (n times) = nc. |
The sum of consecutive numbers
In the Appendix to Arithmetic, we saw that the sum of consecutive numbers -- a triangular number -- is given by this formula:
½n(n + 1),
where n is the last number in the sum. That is,
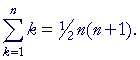
Example 4. Cite the theorems of summation to prove:
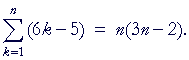
| Proof. | 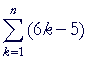 |
= | 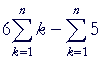 |
Theorems 1 and 2 |
| = | 6· ½n(n + 1) − 5n. | The sum and Theorem 3 | ||
| = | 3n2 + 3n − 5n | |||
| = | 3n2 − 2n | |||
| = | n(3n − 2). | |||
Remainder classes modulo m
Upon division of a number by 3, for example, the remainder will be either 0, 1, or 2.
Here is the remainder class with remainder 0:
3 6 9 12 15 18 . . .
Algebraically, these are the number 3k. k = 1, 2, 3, . . .
We say that these are the numbers congruent to 0 modulo 3.
Here is the remainder class with remainder 1:
1 4 7 10 13 . . .
These are the numbers 3k + 1 -- or, to begin with k = 1, they are the numbers 3k − 2. For to be 1 more than a multiple of 3 is equivalent to being 2 less.
These are the numbers congruent to 1 modulo 3.
Finally, here is the remainder class with remainder 2:
2 5 8 11 14 17 . . .
These are the numbers 3k − 1.
These are the numbers congruent to 2 (or to −1) modulo 3.
Those are the three remainder classes modulo 3, that is, upon division by 3.
Problem 5.
a) Upon division by 5, what are the possible remainders?
0, 1, 2, 3, 4.
b) Write the first four numbers of each remainder class.
5 10 15 20
1 6 11 16
2 7 12 17
3 8 13 18
4 9 14 19
c) Indicate each remainder class algebraically, and let each one begin
c) with k = 1.
5k
5k − 4
5k − 3
5k − 2
5k − 1
An arithmetic series
An arithmetic series is a sum in which each term is generated from the previous term by adding the same number. That number is called the constant difference.
2 + 5 + 8 + 11 + 14 + . . . + 32.
The sum of consecutive numbers in a remainder class is an arithmetic series. 3 is the constant difference. It is the modulo of the remainder class.
Example 5. Prove: 2 + 5 + 8 + 11 + 14 + . . . + (3n − 1) = ½n(3n + 1).
Solution. Those are the numbers with remainder 2 upon division by 3. They have the algebraic form 3k − 1. Therefore we are to prove:
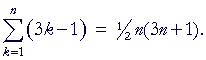
Here is the proof:
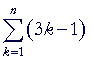 |
= | 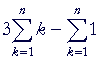 |
Theorems 1 and 2. |
| = | 3· ½n(n + 1) − n. | The sum and Theorem 3. | |
| = | on adding those fractions. | ||
| = | 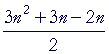 |
||
| = | 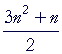 |
||
| = | ½n(3n + 1). | ||
Problem 6. Prove: Every square number is the sum of consecutive odd numbers.
That is,
1 + 3 + 5 + . . . + (2n − 1) = n2.
Proof:
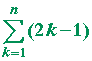 |
= | 2· ½n(n + 1) − n = n2 + n − n = n2. |
That is Problem 3 in Topic 27, Mathematical induction. And in the Appendix to Arithmetic, we explain directly why that is true.
Problem 7. Prove:
1 + 5 + 9 + . . . + (4n − 3) = n(2n − 1).
Proof:
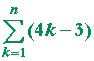 |
= | 4· ½n(n + 1) − 3n |
| = | 2n2 + 2n − 3n | |
| = | 2n2 − n | |
| = | n(2n − 1). | |
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
