21
ALGEBRAIC FRACTIONS
The principle of equivalent fractions
FRACTIONS IN ALGEBRA are often called rational expressions. (See Topic 18 of Precalculus.) We begin with the principle of equivalent fractions, which appears as follows:
| x y |
= | ax ay |
"Both the numerator and denominator may be multiplied
by the same factor."
Both x and y have been multiplied by the factor a.
| x y |
and | ax ay |
are called equivalent fractions. |
That means that, in a calculation, we could replace either one with the other.
It is the same rule as in arithmetic:
| 2 3 |
= | 10 15 |
on multiplying both 2 and 3 by 5.
Problem 1. Write the missing numerator.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| 6 n |
= |
18 3n |
The denominator has been multiplied by 3; therefore the numerator will also be multiplied by 3.
Problem 2. Write the missing numerator.
| 4 x |
= |
4x x2 |
The denominator has been multiplied by x; therefore the numerator will also be multiplied by x.
Problem 3. Write the missing numerator.
| m x |
= |
8x2m 8x3 |
The denominator has been multiplied by 8x2; therefore the numerator will also be multiplied by 8x2.
The student should expect that the original denominator on the left will be a factor of the new denominator on the right. It must be a factor because to produce the new denominator, the original denominator was multiplied.
Problem 4. Write the missing numerator.
("The denominator has been multiplied by _____. Therefore the numerator will also be multiplied by ____.")
| a) | a b |
= |
5a 5b |
b) | 3 x |
= |
6 2x |
c) | 5 y |
= |
5y y2 |
||
| d) | 8 x |
= |
8y xy |
e) | a x |
= |
2x2a 2x3 |
f) | b y |
= |
bx2y x2y2 |
||
| g) | p q |
= |
prs qrs |
h) | 2 b |
= |
2ac abc |
i) | 4 x |
= |
4(x + 1) x(x + 1) |
||
| Example 1. | a | = | ? b |
| Solution. To explain the solution, we will write a as | a 1 |
. |
| a 1 |
= | ab b |
Since 1 has been multiplied by b, then so will a.
The numerator ab however is simply the product of a times b. It is a kind of cross-multiplying, and the student should not have to write the denominator 1.
| a | = | ab b |
You do algebra with your eyes.
Problem 5. Write the missing numerator.
| a) | x | = |
3x 3 |
b) | 2 | = |
2ab ab |
c) | x | = |
x³ x2 |
||
| d) | 1 | = |
x x |
e) | 2 | = |
2x + 2 x + 1 |
f) | x + 1 | = |
x2 − 1 x − 1 |
Part f) is The Difference of Two Squares.
There will be more problems of this type at the 2nd Level.
Reducing to lowest terms
The numerator and denominator of a fraction are called its terms. Since we may multiply both terms, then, symmetrically, we may divide both terms.
| ax ay |
= | x y |
"Both the numerator and denominator may be divided
by a common factor."
When we do that, we say that we have reduced the fraction to its lowest terms.
Again, this is the same as in arithmetic.
| Example 2. Reduce | 5x 5y |
. |
| Answer. | 5x 5y |
= | x y |
. |
5 is a common factor of the numerator and denominator. Therefore we may divide each of them by 5.
One often hears that we have "canceled" the 5's. But that can be very dangerous expression, as the following examples will show.
| Example 3. Reduce | 5 + x 5 + y |
. |
Answer. This can not be reduced. We cannot "cancel" the 5's, because 5 is not a factor of either the numerator or the denominator. In both of them, 5 is a term.
We cannot cancel terms.
The word term does double duty in algebra. We speak of the terms of a sum and also the terms of a fraction, which are the numerator and denominator. A fraction is in its lowest terms when the terms -- the numerator and denominator -- have no common factor.
| Example 4. Reduce | 3a + 6b + 9c 12d |
. |
Answer. When the numerator or denominator is made up of a sum, then if every term has a common factor, we may divide every term by it.
In this example, every term in both the numerator and denominator has a factor 3. Therefore, upon dividing every term by 3, we can write immediately:
| 3a + 6b + 9c 12d |
= | a + 2b + 3c 4d |
There is no more reducing. The numerator and denominator no longer have a common factor.
We could show the common factor explicitly, by writing
| 3a + 6b + 9c 12d |
= | 3(a + 2b + 3c) 3·4d |
But to actually write that is not required.
This example illustrates the following:
To divide a sum -- 3a + 6b + 9c -- by a number,
we must be able to divide every term by that number.
| Example 5. Reduce | 3a + 6b + 8c 12a |
. |
Answer. Not possible. The numerator and denominator have no common factor. 3 is not a common factor, because 3 is not a factor of 8. 2 is not a common factor, because 2 is not a factor of 3. And a is not a common factor. That fraction is in its lowest terms.
To write
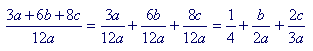
although algebraically correct, is not called reducing. To reduce a fraction means to keep it as one fraction. Otherwise, every fraction could be "reduced."
![]()
| 5 18 |
cannot be reduced. |
Again, to divide a sum, every term must have a common factor, as in Example 4.
| Example 6. Reduce | 8x 8x + 10 |
. |
Answer. 2 is a factor of every term in both the numerator and denominator. Therefore we may divide every term by 2.
| 8x 8x + 10 |
= | 4x 4x + 5 |
. |
There is no more dividing. We cannot "cancel" the 4's because 4 is not a factor of the denominator. 4 is not a factor of 5.
Problem 6. Reduce to lowest terms.
| a) | 3a 3b |
= |
a b |
b) | 8xy 12x |
= |
2y 3 |
c) | 56y 77xy |
= |
8 11x |
| d) | 2x + 6 4x + 8 |
= | x + 3 2x + 4 |
| on dividing every term in both the numerator and denominator by 2. | |||
| e) | 2x + 3 4x + 9 |
= | Not possible. |
| The terms of the numerator and denominator have no common factor. | |||
| Example 7. Reduce | x 4x |
. |
| Answer. | x 4x |
= | 1 4 |
, |
on dividing both the numerator and denominator by x.
Note that we must write 1 in the numerator, for x = 1 · x.
| Example 8. Reduce | 4x x |
. |
| Answer. | 4x x |
= | 4. |
It is not the style in algebra to write 1 as a denominator.
| Example 9. Reduce | x − 3 6(x − 3) |
. |
| Answer. | x − 3 6(x − 3) |
= | 1 6 |
. |
We can view x − 3 as a factor of the numerator, because
x − 3 = (x − 3)·1
Again, we must write 1 in the numerator.
Problem 7. Reduce.
| a) | 2a a |
= | 2 | b) | a ab |
= | 1 b |
c) | 2x 8xy |
= | 1 4y |
| d) | 5(x − 2) x − 2 |
= | 5 | e) | x + 1 2(x + 1) |
= |
1 2 |
f) | 3(x + 2)x 6(x + 2)xy |
= |
1 2y |
| Example 10. Reduce | 15x 5x − 3 |
. |
Answer. Not possible. The numerator and denominator have no common factor.
| Example 11. Reduce | x2 − x − 6 x2 − 4x + 3 |
. |
Answer. In its present form, there is no reducing -- because there are no factors. But we can make factors:
| x2 − x − 6 x2 − 4x + 3 |
= | (x − 3)(x + 2) (x − 3)(x − 1) |
= | x + 2 x − 1 |
(x −3) is now seen to be a common factor. We can divide by it. And when we do, the numerator and denominator no longer have a common factor. The end.
| Example 12. Reduce: | 4x³ − 9x2 4x³ + 6x2 |
. |
Answer. The only common factor is x2. And we could display it by factoring both the numerator and denominator:
| 4x³ − 9x2 4x³ + 6x2 |
= | x2(4x − 9) 2x2(2x + 3) |
= | 4x − 9 2(2x + 3) |
The fraction is now in its lowest terms. No common factors.
Problem 8. Reduce.
| a) | 5x 10x + 15 |
= |
5x 5(2x + 3) |
= |
x 2x + 3 |
| b) | 3x − 12 3x |
= |
3(x − 4) 3x |
= |
x − 4 x |
| c) | 12x − 18y + 21z 6y |
= |
4x − 6y + 7z 2y |
, |
upon dividing every term by their common factor, 3.
| d) | 2m m2 − 2m |
= |
2m m(m − 2) |
= |
2 m − 2 |
| e) | x2 − x x |
= |
x(x − 1) x |
= | x − 1 |
| f) | 12x2 16x5 − 20x2 |
= |
12x2 4x2(4x3 − 5) |
= |
3 4x3 − 5 |
| g) | x + 3 4x + 12 |
= |
x + 3 4(x + 3) |
= |
1 4 |
| h) | 2x − 8 x − 4 |
= |
2(x − 4) x − 4 |
= | 2 |
| i) | 2x − 2y 3x − 3y | = |
2(x − y) 3(x − y) |
= |
2 3 |
Problem 9. Make factors and reduce.
| a) | x2 − 2x − 3 x2 − x − 2 |
= |
(x + 1)(x − 3) (x + 1)(x − 2) |
= |
x − 3 x − 2 |
| b) | x2 + x − 2 x2 − x − 6 |
= |
(x + 2)(x − 1) (x + 2)(x − 3) |
= |
x − 1 x − 3 |
| c) | x2 − 2x + 1 x2 − 1 |
= |
(x − 1)2 (x + 1)(x − 1) |
= |
x − 1 x + 1 |
| d) | x2 − 100 x + 10 |
= |
(x + 10)(x − 10) x + 10 |
= | x − 10 |
| e) | x + 3 x2 + 6x + 9 |
= |
x + 3 (x + 3)2 |
= |
1 x + 3 |
| f) | x³ + 4x2 _ x2 + x − 12 |
= |
x2(x + 4) (x − 3)(x + 4) |
= |
x2 x − 3 |
Problem 10. Reduce to lowest terms -- if possible.
| a) | 3 + x 3x |
Not possible. | |
| The numerator and denominator have no common factors. | |||
| b) | 8a + b 2ab |
Not possible. Again, no common factors. |
| c) | 8a + 2b 2ab |
= |
2(4a + b) 2ab |
= |
4a + b ab |
| d) | 6a + b 3a + b |
Not possible. | |
| The numerator and denominator have no common factors. 3 is not a factor of either the numerator or denominator. It is a factor only of the first term in each. | |||
| e) | 6(a + b) 3(a + b) |
= | 2 |
| f) | 2x + 4y + 6z 10 |
= |
x + 2y + 3z 5 |
Divide every term by 2. |
| g) | 2x + 4y + 5z 10 |
Not possible. | |
| The numerator and denominator have no common factors. | |||
| h) | (x + 1) + (x + 2) (x + 1)(x + 3) |
Not possible. | |
| The numerator is not made up of factors. | |||
| i) | (x + 1)(x + 2) (x + 1)(x + 3) |
= |
x + 2 x + 3 |
| j) | ab + c abc |
= | Not possible. |
| The numerator and denominator have no common factors. | |||
| k) | ab + ac abc |
= |
a(b + c) abc |
= |
b + c bc |
| l) | x2 − x − 12 x2 + x − 6 |
= |
(x + 3)(x − 4) (x + 3)(x − 2) |
= |
x − 4 x − 2 |
Next Lesson: Multiplying and dividing algebraic fractions
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2022 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
