9
COMMON MEASURE
WE SAY THAT A SMALLER MAGNITUDE measures a larger (or an equal) one if the larger magnitude is its multiple.

If the straight line FG is the fourth multiple of the straight line E, then we say that E measures FG four times.
"Measures", in geometry, is like "is a divisor of" in arithmetic.
Problem 1. In this figure, all the segments are equal.
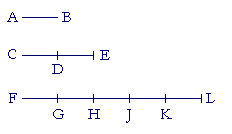
a) How many times does AB measure CE?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Twice.
b) How many times does AB measure FL?
Five times.
c) Does CE measure FL?
No. FL is not a multiple of CE.
d) Does CE measure FK?
Yes. Twice.
e) Does AB measure FK?
Yes. Four times.
Problem 2. Borrowing the word measure from geometry:
| a) Does 3 measure 12? | Yes. Four times. | |||
| b) Does 3 measure 11? | No. | |||
| c) Does 5 measure 30? | Yes. | |||
| d) Does 8 measure 30? | No. | |||
Problem 3. Name the first five multiples of ½ inch.
½ in, 1 in, 1½ in, 2 in, 2½ in.
Problem 4. Let a straight line be 1½ meters long.
a) Does a straight line ½ meter long measure it?
Yes.
a) How many times?
Three times.
b) Does a straight line 1 meter long measure it?
No. 1½ meters is not a multiple of 1 meter.
Common measure
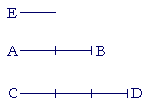
E is a common measure of AB and CD. E measures AB two times, and it measures CD three times.
If E were 1 inch, then AB would be two inches and CD would be three inches.
| If E were | 1 4 |
inch, then AB would be | 2 4 |
or | 1 2 |
inch, and CD would be |
| 3 4 |
inch. |
Thus, magnitudes have a common measure when each of them is a multiple of the same unit. What could that unit be? It could be either the unit of measure itself, such as 1 inch, or one of its unit fractions, such as ¼ inch.
In particular:
Every rational number has a common measure with 1.
For, every rational number -- every fraction -- is a multiple of some unit fraction. And 1 is a multiple of every unit fraction. (Lesson 6.)
Problem 5.
| a) Do 1 inch and 2 | 3 8 |
inches have a common measure? |
Yes. 1/8 inch.
b) Which multiple of the common measure is 1 inch, and which
| multiple is 2 | 3 8 |
inches? |
| 1 inch = 8 × | 1 8 |
inch. 2 | 3 8 |
inches = 19 × | 1 8 |
inch. |
c) Express the ratio of those lengths as a ratio of natural numbers.
| 1 inch : 2 | 3 8 |
inches = 8 : 19 |
Problem 6.
a) What length is a common measure of 1 meter and 3.72 meters?
.01 meters
b) Which multiples of the common measure are those lengths?
1 m = 100 × .01 m. 3.72 m = 372 × .01 m.
c) Proportionally, 1 meter : 3.72 meters = 100 : 372
Problem 7. If the unit of measure is 1 mile, and L is a straight line, then what are the possible common measures of 1 mile and L?
1 mile itself, or one of its unit fractions.
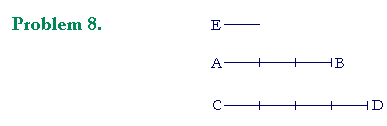
E is a common measure of AB and CD. It measures AB three times, and CD four times.
a) If E is 1 meter, then how long are AB and CD?
AB = 3 m. CD = 4 m.
b) If E is ½ meter how long are AB and CD?
AB = 1½ m. CD = 2 m.
c) If E is one-thousandth of a meter, how long are AB and CD?
AB = .003 m. CD = .004 m.
d) In any case, AB is to CD in the same ratio as which two natural
d) numbers?
AB : CD = 3 : 4
We can now state the following theorem:
Theorem. Magnitudes (of the same kind) will have a common measure if and only if they have the same ratio as natural numbers.
This should be obvious, because each magnitude will be a multiple of their common measure.
Again,
Problem 9. What is "the ratio of natural numbers"?
One number is a multiple of the other, a part of it, or parts of it.
Problem 10. AB, CD are straight lines, and AB is two fifths of CD.
a) Illustrate that.
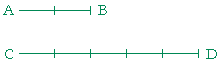
b) Do AB, CD have a common measure?
Yes. They are in the same ratio as two natural numbers.
c) Which multiples of it are AB, CD? AB : CD = 2 : 5
d) If AB is 1 cm, then how long is their common measure?
½ cm
How long then is CD? 5 × ½ = 2½ cm.
Problem 11. EF is four times longer than GH.
a) Illustrate that.
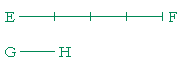
b) Do they have a common measure?
Yes. They are in the same ratio as two natural numbers.
c) What is their common measure? GH
Problem 12. Show that each of these is to 1 meter in the same ratio as two natural numbers. In each case, what length is their common measure?
a) 3 meters.
3 m : 1 m = 3 : 1. Their common measure is 1 meter.
b) 3¼ meters.
3¼ m : 1 m = 13/4 : 1 = 13 : 4.
Their common measure is ¼ meter.
c) 0.512 meters.
0.512 m : 1 m = 512 : 1000.
Their common measure is .001 meter.
d) 9.999999 meters.
9.999999 m : 1 m = 9,999,999 : 1,000,000.
Their common measure is .000001 meter.
Problem 13. The following three statements refer to the same fact. Do you see that?
AB is a rational number of units.
AB and the unit of measure have a common measure.
AB and the unit have the same ratio as two natural numbers.
a) Illustrate those statements when AB is 2¼ inches.
2¼ is a rational number.
¼ inch is the common measure of AB and 1 inch.
AB : 1 inch = 2¼ : 1 = 9/4 : 1 = 9 : 4
b) Illustrate them when AB is .59 meters.
.59 is a rational number.
.01 m is the common measure of AB and 1 m.
AB : 1 m = .59 : 1 = 59 : 100
Problem 14. This rectangle is three fourths of that one.
![]()
Do they have a common measure of area?
Yes. They are in the same ratio as two natural numbers.
What magnitude is their common measure?
The third part of the smaller rectangle, or, equivalently, the fourth part of the larger.
![]()
Problem 15. This square is half the area of the circle. Do they have a common measure of area?
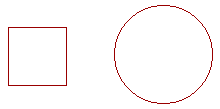
Yes. They are in the same ratio as two natural numbers. If it takes one can of paint to paint the square, then it will take exactly two cans to paint the circle.
Next Topic: Squares and their sides
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2020 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
