13
THE EXISTENCE
OF
IRRATIONAL NUMBERS
This continues the previous Lesson.
NO ONE HAS EVER BEHELD the actual value of ![]() , or π, or any irrational number. All we ever generate are rational approximations -- even to hundreds of thousands of decimal places. In what sense, then, are the irrationals themselves numbers? We may not assume that just because something has been defined and given name and a symbol, that it is something that actually exists. (A dragon has been defined. Do dragons exist?)
, or π, or any irrational number. All we ever generate are rational approximations -- even to hundreds of thousands of decimal places. In what sense, then, are the irrationals themselves numbers? We may not assume that just because something has been defined and given name and a symbol, that it is something that actually exists. (A dragon has been defined. Do dragons exist?)
The Greeks did not admit irrational numbers. They were quite content to say that incommensurable magnitudes simply are not in the same ratio as two natural numbers. That did not prevent them from approximating the number we call ![]() , just as we must if we want to know it and use it.
, just as we must if we want to know it and use it.
Modern mathematics, on the other hand, is virtually based on calculating with symbols for the irrationals. For with those symbols -- ![]() , π, and so on -- mathematicians and scientists can perform written calculations that previously were impossible. As far as the mathematics of measurement is concerned, calculation with symbols for irrationals has been the main logical development since the 3rd century, B.C.
, π, and so on -- mathematicians and scientists can perform written calculations that previously were impossible. As far as the mathematics of measurement is concerned, calculation with symbols for irrationals has been the main logical development since the 3rd century, B.C.
Knowledge of irrational numbers
Arithmetic is knowledge of numbers. Knowledge not only of how to calculate with numbers, but knowledge of their properties. A number has not only its properties as an individual, such as being even or odd, or prime. It has its properties in the society of numbers, which is how it relates to others. What is its position in the sequence? 5 comes before 6 and after 4. 6.184 is less than 6.185, and more than 6.183. That is what makes a number different from other numbers. It has a different relative position. That is the essence of being a number.
For an irrational number to exist, then -- for it to be a number -- we must be able to place it with respect to order relative to any rational number. For the rational numbers are what we definitely know.
Is ![]() , then, less than or greater than 1.41?
, then, less than or greater than 1.41?
We can compare them by squaring. (![]() )2 = 2. (1.41)2 = 1.9881. Therefore,
)2 = 2. (1.41)2 = 1.9881. Therefore, ![]() is greater than 1.41.
is greater than 1.41.
Is ![]() less than or greater than 1.42?
less than or greater than 1.42?
(1.42)2 = 2.0164. Therefore, ![]() is less than 1.42.
is less than 1.42.
We have found, then, that ![]() falls between 1.41 and 1.42 --
falls between 1.41 and 1.42 --
1.41 < ![]() < 1.42.
< 1.42.
Continuing to the third decimal digit, we would find
1.414 < ![]() < 1.415.
< 1.415.
In this way, we could place ![]() with respect to order relative to any rational number. We may say then that
with respect to order relative to any rational number. We may say then that ![]() is, in fact, a number.
is, in fact, a number.
Thus if the symbol for an irrational number is to refer to something that actually exists, then there must be a method to compute its decimal approximation to as many decimal digits as we please; for we could then place it with respect to order relative to any rational number. That is true, for example, of π. π is approximately
3.1415926535897932384626433.
Real numbers
We have two ideas of number.
1) Number as discrete units. These are the numbers whose names we use for counting. They are the natural numbers.
2) Number as measurement. These are the numbers whose names we need for measuring. They are the rationals and irrationals.
The technical term for number as measurement is real number.
Here are 6 discrete units,
//////
which, we must be admit, is our fundamental idea of 6.

The line AB is a picture of the real number 6, in the sense that if AE is the unit, then, proportionally,
AB : AE = 6 : 1.
We require a real number, then, to name the distance of a point P from 0 on the number line.
![]()
We have seen that the rational numbers are not sufficient for that task, because lengths can be incommensurable. Irrational numbers therefore became necessary.
Problem 1. In terms of parts, what is the difference between the natural number 10 and the real number 10?
The natural number 10 has only half, a fifth part, and a tenth part. The real number 10 could be divided into any parts.
Problem 2. We have classified numbers as rational, irrational, and real. Name all the categories to which each of the following belongs.
| a) 2 | Real, rational. | b) | 3 5 |
Real, rational. |
| c) 11 | 1 9 |
Real, rational. | d) |
Real, irrational. |
e) Cube root of 8 = 2. Real, rational.
f) Cube root of 9. Real, irrational.
g) 3.1415926535897932384626433
Real, rational. Every decimal is
g) rational. This decimal is an approximation to pi.
| h) |
i) |
j) Fourth root of 10. Real, irrational.
*
So. We can now return to the question we posed at the beginning of this inquiry:
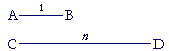
If AB, CD are lengths, will there always be a number n, rational or irrational, such that, proportionally,
AB is to CD as 1 is to n?
Can we always name the ratio -- the relationship -- that any length will have to the unit of length? For, numbers have names. That is their usefullness: 1, 9.6, ![]() ,
, ![]() .
.
But names are discrete while lengths are continuous. Any claim, then, that there is a number to name every length will require that the names themselves be continuous. A continuum of lengths make sense. But a continuum of names is an absurdity.
Or are there "numbers" with no names? If so, then they will be "numbers" that are not the measures of anything. They will be "numbers" of which we have no knowledge -- which we could never place with respect to order. In other words, they would not be numbers. Or rather, the word number would then have a very different and unaccustomed meaning.
Just as all the words in a dictionary are no match for all of reality, so the names of numbers can never exhaust the lengths of lines. That is the separation of arithmetic and geometry: It is not possible to name every ratio of magnitudes.
(See Are the real numbers really numbers?)
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2020 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
