Lesson 15
PARTS
OF NATURAL NUMBERS 1
In this chapter we will learn to speak the language of arithmetic. This will allow us to relate any two numbers. We will learn to say, for example, that 6 is the fourth part, or one quarter, of 24, and that 18 is three quarters of 24. We are not concerned here with "How do you do it?" but, rather, "What does that mean?"
What is more, to really understand Percent, it is necessary to understand parts, because a percent is a part of 100%. 50% means half -- because 50 is half of 100. 25% means a quarter beause 25 is a quarter of 100. And 20% means a fifth because 20 is the fifth part of 100.
Finally, fractions (Lesson 20) are parts of number 1.
In this Lesson, we will answer the following:
- What is a natural number?
- What do we mean by the multiples of a number?
- What does it mean to say that a smaller number is a part of a larger number?
- How can we calculate a part of a number?
- What does it mean to say that a smaller number is parts of a larger number?
- How can we calculate parts of a number?
| 1. | What is a natural number? |
| It is a collection composed of indivisible units of the same kind. | |
| To those collections we give a sequence of names and symbols. | |
1, 2, 3, 4, and so on, are the familiar numerals for the natural numbers. We calculate with those symbols, and so it has become conventional to call the symbols themselves "numbers." Yet a symbol is not what it symbolizes, what it stands for, which in this case is a number of discrete units.
By a number in what follows, we will mean a natural number.
Cardinal and ordinal
The natural numbers have two forms: cardinal and ordinal. The names of the cardinal numbers are:
One, two, three, four; and so on.
They answer the question How many?
The names of the ordinal numbers are:
First, second, third, fourth; and so on.
They answer the question Which one? We will see that those ordinal numbers express division into equal parts. With the exception of "half," an ordinal number will name which part: the third part, the fourth, the fifth, and so on.
To each cardinal number except 1, there corresponds the name of a part.
| 2 | Half | |
| 3 | Third | |
| 4 | Fourth | |
| 5 | Fifth |
And so on.
| 2. | What do we mean by the multiples of a number? |
| They are the numbers produced when that number is repeatedly added. | |
Here are the first few multiples of 5:
5, 10, 15, 20, 25, 30, 35, 40.
5 is the first multiple of 5; 10 is the second multiple; 15, the third; and so on.
| 3. | What does it mean to say that a smaller number is a part of a larger number? |
| It means that the larger number is a multiple of the smaller. Equivalently, the smaller is contained in the larger an exact number of times. | |
5, then, will be a certain part of each one of its multiples.
5, 10, 15, 20, 25, 30, 35, 40.
Since 15 is the third multiple of 5, we say that 5 is the third part of 15.
We use that same ordinal number to name the part.
Since 20 is the fourth multiple of 5, we call 5 the fourth part of 20. 5 is the fifth part of 25, the sixth part of 30; and so on. But, 5 is half of 10. (We do not say the second part.) And 5 is not a part of itself; there is no such thing as the first part.
So with the exception of "half," an ordinal number names into which parts a number has been divided.
![]()
15 has been divided into Thirds; that is, into three equal parts. The third part of 15 is 5.
This use of ordinal numbers does not imply a sequence: the first part, the second, the third, and so on. See below.
If we divide a number into four equal parts,
![]()
then we have divided it into fourths (or quarters); if into five equal parts,
![]()
into fifths. But if we divide into two equal parts, then we have divided it in half.
It is important to understand that we are not speaking here of proper fractions -- numbers that are less than 1 and that we need for measuring. We are explaining how the ordinal numbers --- third, fourth, fifth, etc. -- name into which parts a number has been divided. When answering the questions of this Lesson, the student should not write fractions. We will come to those symbols in Lesson 20.
It should be clear that the ordinal names of the parts belong to language itself, and are prior to the names of the proper fractions, which are the parts of 1.
Why is the number we write as 1 over 3 -- ![]() - called "one-third"? Because the numerator is one third -- the third part -- of the denominator.
- called "one-third"? Because the numerator is one third -- the third part -- of the denominator.
p![]()
That must be understood first. We can then explain that the number we call ![]() is the third part of 1.
is the third part of 1.
p![]()
Example 1. 3 is which part of 18?
![]()
Answer. The sixth part. 3 is contained in 18 six times.
Note that 1 is a part of every number (except itself) because every number is a multiple of 1. Which part is it? The part that says the number's name.
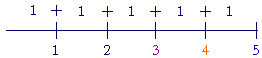
1 is the third part of 3, the fourth part of 4, the fifth part of 5, the hundredth part of 100. 1 is half of 2.
Example 2. What number is the fourth part, or a quarter, of 28?
Answer. 7. Because 28 is made up of four sevens.
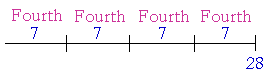
Four times 7 is 28.
7 is the fourth part of 28.
Example 3. 2 is the fifth part of what number?
Answer. 10. Because five 2's are 10.

Every number is the fifth part of five times itself ![]()
4 is the fifth part of 5 × 4, which is 20.
9 is the fifth part of 5 × 9, which is 45.
20 is the fifth part of 5 × 20, which is 100.
| 4. | How can we calculate a part of a number? |
| Divide by the cardinal number that corresponds to the name of the part. To take half of a number, divide by 2. To take a third, divide by 3. And so on. | |
See Lesson 11, Question 2, and especially Example 6.
Example 4. How much is an eighth of $72?
Answer. 72 ÷ 8 = 9. An eighth of $72 is $9.
Example 5. Tenths, hundredths. How much is a tenth of $275?
How much is a hundredth?
Answer. To find a tenth, divide by 10.
275 ÷ 10 = 27.5
Since this is money, we report the answer as $27.50. (Lesson 3.)
As for a hundredth, we will separate two decimal digits:
$275 ÷ 100 = $2.75
In Lesson 4, we saw that when we divide by 10, we have taken 10% of the number. And when we divide by 100, we have taken 1%.
Therefore, 10% of $275 is $27.50. 1% is $2.75.
Note: Whenever we divide by any power of 10 -- the digits do not change.
275 ÷ 100 = 2.75
Conversely, then, if two numbers have the same digits, they differ by a power of 10.
Example 6. $85 is which part of $850?
Answer. Apart from the 0 at the end of $850, those numbers have the same digits. Therefore, they differ by a power of 10. 850 is in fact 10 times 85. (Lesson 4, Question 1.) Therefore, $85 is the tenth part of $850. To say the same thing, $85 is 10% of $850.
Example 7. $.98 is which part of $98?
Answer. They have the same digits. They differ by a power of 10.
$.98 is the hundredth part of $98. It is 1% of it.
Divisors
We say that a smaller number is a divisor of a larger number if the larger number is its multiple. We say however that a number is a divisor of itself.
Here, for example, are all the divisors of 6:
1, 2, 3, 6.
4 is not called a divisor of 6, because 6 is not a multiple of 4.
With the exception of the number itself: The divisors of a number are the only parts that a number has.
1 is the sixth part of 6. 2 is the third part of 6. 3 is half of 6.
Those are the only parts that 6 has.
Example 8. Find all the divisors of 30 in pairs. Each divisor (except 30) is which part of 30?
Answer. Here are all the divisors of 30 in pairs:
1 and 30. (Because 1 × 30 = 30.)
2 and 15. (Because 2 × 15 = 30.)
3 and 10. (Because 3 × 10 = 30.)
5 and 6. (Because 5 × 6 = 30.)
On naming which part of 30, each divisor will say the ordinal name of its partner:
1 is the thirtieth part of 30.
2 is the fifteenth part of 30. 15 is half of 30.
3 is the tenth part of 30. 10 is the third part of 30.
5 is the sixth part of 30. 6 is the fifth part of 30.
Divisors always come in pairs. And that implies the following:
Theorem. For every divisor (except 1) that a number has, it will have a part with the ordinal name of that divisor.
(Euclid, VII. 37.)
Since 18, for example, has a divisor 3, then 18 has a third part. Since 18 has a divisor 6, then 18 has a sixth part. But 18 does not have a fifth part, because 5 is not a divisor of 18.
Here is an illustration that 18 has a divisor 3:
![]()
18 = 6 × 3.
But according to the order property of multiplication:
18 = 3 × 6.
![]()
This shows that 6 -- the partner of 3 -- is the third part of 18.
In other words, since 18 has a divisor 3, then 18 has a third part.
Example 9. Into which parts could 12 people be divided?
Answer. The divisors of 12 are
1, 2, 3, 4, 6, and 12.

Corresponding to each divisor (except 1), there will be a part with the ordinal name of the divisor. 12 people, therefore, could be divided into
Halves, thirds, fourths, sixths, and twelfths.
You cannot take a fifth of 12 people. 12 does not have a divisor 5.
Percent: Parts of 100%
A percent is another way of naming a part. Because whatever part the percent is of 100%, that is the part we are naming.
Since 50% is half of 100%, then 50% means half. 50% of 12 -- half of 12 -- is 6.
Since 25% is a quarter, or a fourth, of 100% --
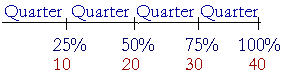
-- then 25% is another way of saying a quarter. 25% of 40 -- the fourth part of 40 -- is 10.
In the next Lesson, Question 10, we will see how to take 25% by taking half of half.
Since 20% is the fifth part of 100% --

(100 is made up of five 20's) -- then 20% is another way of saying a fifth. 20% of 15 -- the fifth part of 15 -- is 3.
In the next Lesson we will see that 33![]() % means a third.
% means a third.
Repeated division in half
Every time we take half of something, we get twice as many parts. Half of a whole --

-- results in two equal parts. Each part is Half.
If we divide each Half in half --

-- the whole will be in four equal parts, or Quarters.
If we divide each Quarter in half --

-- the whole will then be in twice as many, that is, eight equal parts, or Eighths.
Half of an Eighth is a Sixteenth. Half of a Sixteenth is a Thirty-second. And so on.
Now, here are the number of equal parts that result when we repeatedly take half:
2, 4, 8, 16, 32, 64, and so on.
Those numbers are called the powers of 2. Repeated division in half is very common. The student should know the names of the sequence of those parts:
Halves, Quarters, Eighths, Sixteenths, Thirty-seconds, and so on.
*
When we say "5 is the third part of 15," we do not imply a sequence: the first part, the second part, the third, and so on. When we speak of the third part, that is a different meaning for the word "third." It means each one of three equal parts that together make up the whole.
![]()
We say that we have divided 15 into thirds.
Yet "third" still retains its ordinal character. Because to the question, "Which part of 15 is 5?", we answer,
"The third part." We use that ordinal number because 15 is the third multiple of 5.
At this point, please "turn" the page and do some Problems.
or
Continue on to the next Section: Parts, plural
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
