3
FUNCTIONS
Functional notation:
The argument of the function
What is a function?
WHEN ONE THING DEPENDS on another, as for example the area of a circle depends on the radius—when the radius changes, the area will change—then we say that the first is a "function" of the other. The area of a circle is a function of—it depends on—the radius.
Mathematically:
A rule that relates two variables, typically x and y,
is called a function
if to each value of x the rule assigns one and only one value of y.
When that is the case, we say that y is a function of x.
Thus a "function" must be single-valued ("one and only one"). For example,
y = 2x + 3.
To each value of x there is a unique value of y.
Domain and range
The values that x may assume are called the domain of the function. We say that those are the values for which the function is defined.
In the function y = 2x + 3, the domain may include all real numbers. x could be any real number. Or, as in Example 1 below, the domain may be arbitrarily restricted.
There is one case however in which the domain must be restricted: A denominator may not be 0. In this function,
| y | = | 1 x − 2 |
, |
x may not take the value 2. For division by 0 is an excluded operation. (Lesson 5 of Algebra.)
Once the domain has been defined, then the values of y that correspond to the values of x are called the range. Thus if 5 is a value in the domain of y = 2x + 3, then 13 (2· 5 + 3) is the corresponding value in the range.
By the value of the function we mean the value of y. And so when x = 5, then we say that the value of the function y = 2x + 3, is 13.
The range is composed of the values of the function.
It is customary to call x the independent variable because we are given, or we must choose, the value of x first. y is then called the dependent variable because its value will depend on the value of x.
Example 1. Let the domain of a function be this set of values:
A = {0, 1, 2, −2}
and let the variable x assume each one. Let the rule that relates the value of y to the value of x be the following:
y = x2 + 1.
a) Write the set of ordered pairs (x, y) which "represents" this function.
Answer. {(0, 1), (1, 2), (2, 5), (−2, 5)}
That is, when x = 0, then y = 02 + 1 = 1.
When x = 1, then y = 12 + 1 = 2. And so on.
b) Write the set B which is the range of the function.
Answer. B = {1, 2, 5, 5}. The values in the range are simply those values of y that correspond to each value of x.
Notice that to each value of x in the domain there corresponds one—and only one—value of the function. Even though the value 5 is repeated, it is still one and only one value.
Example 2. Here is a relationship in which y is not a function of x:
y2 = x
When x = 4, for example—y2 = 4—then y = 2 or −2. To each value of x, there is more than one value of y.
Problem 1. Let y be a function of x as follows:
y = 3x2
a) Which is the independent variable and which the dependent variable?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
x is the independent variable, y is the dependent.
b) The domain of a function are the values of the independent
b) variable, which are the values of x.
c) What is the natural domain of that function?
Since there is no natural restriction on the values of x, the natural domain of that function is any real number. x could take any value on the x-axis.
d) The range of a function are the values of the dependent variable,
d) which are the values of y.
e) What is the range of that function? (Consider that the values of x2
e) are never negative.)
y ≥ 0
f) Write any three values of that function as members of an ordered pair.
For example, (1, 3), (2, 12), (3, 27)
Functional notation
The argument of the function
It is convenient for a function to have a name. The simplest name is a letter such as f. And so let us call the function—the rule—y = x2 + 1 by the name "f." We write:
f(x) = x2 + 1.
We read this,
"f of x equals x2 + 1."
The parentheses in f(x)—"f of x"—do not mean multiplication. They are part of what is called functional notation. f is the name of the function. Whatever appears within the parentheses is called the argument of the function. It is upon the argument that the function called f will "operate."
In trigonometry, the names of the functions are sine, cosine, tangent; and so on. The argument of a trigonometric function will be an angle. sin θ.
Thus, the function f has been defined as follows:
f(x) = x2 + 1.
This means that the function f will square its argument, and then add 1.
For example,
| f(7) | = | 72 + 1 = 50. |
| f(−4) | = | (−4)2 + 1 = 17. |
| f(t) | = | t 2 + 1. |
| f(x + h) | = | (x + h)2 + 1 = x2 + 2xh + h2 + 1. |
(Lesson 18 of Algebra: The square of a binomial.)
The function f having been defined, that is how it will operate on any argument—which is the input. The output is the value of the function. We could illustrate it as follows:
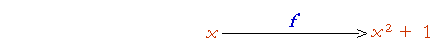
An argument x goes into the f machine. Out comes x2 + 1.
We write
y = f(x).
"y is a function of x, whose name is f."
f(x), then, is the dependent variable. Its value will depend on the value of x. We saw above that when x = 7, f(x) = 50. When x = −4, f(x) = 17. And so on.
A function of a function
Let us now consider a second function whose name will be g.
f(x) = x2 + 1 and g(x) = 5x.
Consider this function,
g(f(x)).
g will operate on f. What does g do to its argument? It simply multiplies the argument by 5. Therefore,
g(f(x)) = g(x2 + 1) = 5(x2 + 1) = 5x2 + 5.
The parentheses in g(x2 + 1) are the parentheses of the functional notation. The parentheses of 5(x2 + 1), however, are the grouping parentheses, which here indicate multiplication.
Now let's look at
f(g(x)).
"f of g of x"
f has g as its argument:
f(g(x)) = f(5x) = (5x)2 + 1 = 25x2 + 1.
Again, f squares its argument and adds 1.
Problem 2. Read each symbol.
| a) f(x) | "f of x" | b) g(x) | "g of x" | |
| c) f(2) | "f of 2" | d) g(−1) | "g of −1" | |
| e) f(x2 − 1) | "f of x2 − 1" | f) f(g(x)) | "f of g of x" | |
Problem 3. Let f(x) = x2 − 1. Evaluate the following.
| a) f(1) | 12 − 1 = 0 | b) f(−2) | 3 | |
| c) f(2/3) | − 5/9 | d) f(− 7/5) | 24/25 | |
Problem 4. Let g(x) = 2 − x. Evaluate the following.
| a) g(0) | 2 | b) g(−1) | 3 | |
| c) g(6) | −4 | d) g(−4) | 6 | |
Problem 5. Let y = f(x) = 1 − x3. What is the value of the function when
| a) x = 0. | y = 1 | b) x = −1. | y = 2 | |
| c) x = q. | y = 1 − q3 | d) x = −q. | y = 1 + q3 | |
Problem 6. Let f(x) = 4x2. Write what results when f operates on each argument.
| a) f(r) | 4r2 | b) f(t) | 4t2 | |
| c) f(x5) | 4x10 | d) f(x − 5) | 4(x − 5)2 = 4x2 −40x + 100 | |
| e) f(1/x2) | 4/x4 | f) f(½ |
x | |
Problem 7. If h(x) = −2, then
| a) | h(x3) = −2 | b) | h(x + 5) = −2 | c) | h(10) = −2 |
The function h operates on every argument the same way. It produces −2.
h is called a constant function, as we will see in Topic 5.
Problem 8. Function of a function. Let f(x) = x2 and g(x) = x + h. Write the function
a) f(g(x)) = f(x + h) = (x + h)2 = x2 + 2xh + h2
b) g(f(x)) = g(x2) = x2 + h
Problem 9. Let f(x) = x − 3, and g(x) = 3 − x. Write the functions
f(g(x)) and g(f(x)).
f(g(x)) = f(3 − x) = (3 − x) − 3 = −x
g(f(x)) = g(x − 3) = 3 − (x − 3) = 3 − x + 3 = 6 − x
Problem 10. Let f(x) = x5 and g(x) = x1/5. Write the functions
f(g(x)) and g(f(x)).
f(g(x)) = f(x1/5) = (x1/5)5= x1= x
g(f(x)) = g(x5) = (x5)1/5 = x
Problem 11. This expression—
| f(x + h) − f(x) h |
—is called the Newton quotient or the difference quotient. Calculating and simplifying it is a fundamental task in differential calculus.
For each function f(x), determine the difference quotient in a simplified form.
a) f(x) = 2x + 1
| 2(x + h) + 1 − (2x + 1) h |
= | 2x + 2h + 1 − 2x − 1 h |
| = | 2h h |
|
| = | 2. | |
b) f(x) = x2
| 1) | (x + h)2 − x2 h |
= | x2 + 2xh + h2 − x2 h |
| 2) | = | 2xh + h2 h |
|
| 3) | = | 2x + h. | |
In Line 1) we squared the binomial x + h.
In Line 2) we subtracted the x2s.
In Line 3) we divided both the numerator and denominator by h.
| c) f(x) = | 1 x |
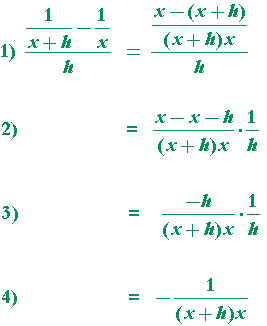
In Line 1) we added the fractions in the numerator of the complex fraction. (Lesson 23 of Algebra.)
In Line 2) we removed the parentheses in the numerator, and multiplied by the reciprocal of the denominator. (Lesson 22 of Algebra.)
In Line 3) we subtracted the x's.
In Line 4) we canceled the h's as −1, which on multiplication with 1 makes the fraction itself negative. (See Lesson 22 of Algebra, Problem 3h.)
Next Topic: Introduction to graphs
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
