5
BASIC GRAPHS
THE FOLLOWING ARE THE GRAPHS that occur throughout analytic geometry and calculus. The student should be able to sketch them -- and recognize them -- purely from their shape. It is not necessary to plot points.
A constant function
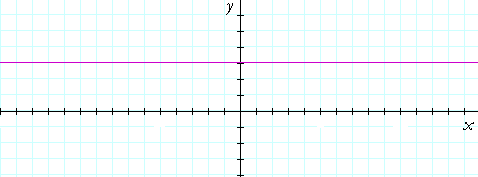
Here is the graph of y = f(x) = 3. It is a straight line parallel to the x-axis. It is called a constant function because to every value of x there corresponds the same value of y: 3.
Is a constant function single-valued? Yes, it is, because to each value of x there is one and only one value of y. 3.
A constant function has the form
y = c ,
where c is a constant, that is, a number.
The identity function and the absolute value function
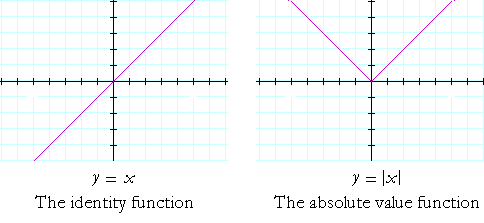
y = x is called the identity function because the value of y is identical with that of x. The coördinate pairs are (x, x).
In the absolute value function, the negative values of y in the identity function are reflected into the positive side. For, |−x| = |x| = x. The coördinate pairs are (x, |x|).
Example.
a) What is the domain of the identity function?
There is no natural restriction on the values of x. Therefore, the domain -- where the function "lives" -- includes every real number.
−
< x <
Note first that infinity "" is not a number and it is not a place. It is a word, together with a symbol, we use to mean: There is no limit to the values of x that we could name.
Note that we write "x less than ." Equal to infinity makes no sense.
b) What is the range of the identity function?
The range are those values of y that correspond to the values in the domain. Inspecting the graph will show that y, also, will take every real value.
− < y <
Parabola and square root function
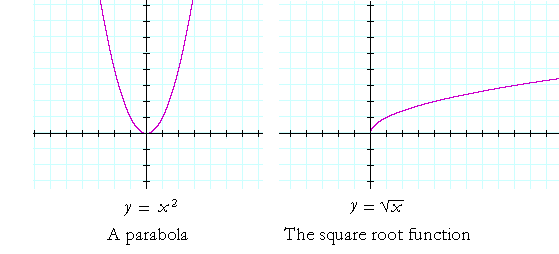
In the parabola y = x2, the coördinate pairs are (x, x2). We can see that the following points are on the graph: (1, 1), (−1, 1), (2, 4), (−2, 4), and so on.
The graph of the square root function is related to y = x2. It is its inverse. The coördinate pairs are (x, 
). For example, (1, 1), (4, 2), (9, 3), and so on.
Note that the square root function is defined only for non-negative values of x. For, the square root of a negative number is not real.
Also, the symbol refers to one non-negative number called the principal square root. (See Lesson 26 of Algebra, Example 2.) y = is therefore a function.
Problem 1. What is the domain of the function y =x2, and what is its range?
This function is defined for all values of x : −∞ < x < ∞.
As for the range, the lowest value of y is 0. And there is no limit to the highest value. 0 ≤ y < ∞.
Problem 2. What is the domain of the square root function, and what is its range?
The square root function is defined only for non-negative values of x. Domain: x ≥ 0.
As for the range, the lowest value of y is 0. And there is no limit to the highest value. 0 ≤ y < ∞.
The cubic function
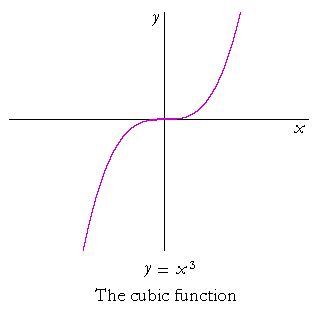
The cubic function is y = x3. When x is negative, y is negative: Odd powers of a negative number are negative.
Problem 3. What is the domain of the cubic function, and what is its range?
Domain: −∞ < x < ∞.
Range: −∞ < y < ∞.
The reciprocal function
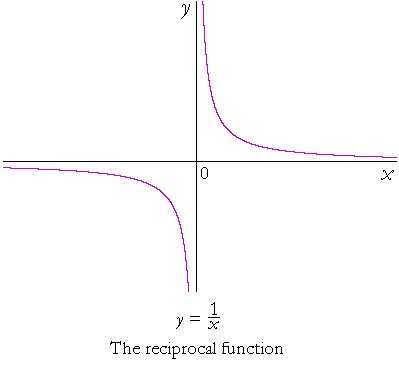
When x is a very large positive number -- on the extreme right of the x-axis -- its reciprocal is a very small positive number. The graph is very close to the x-axis.
When x is a very small positive number -- close to x = 0 -- its reciprocal is a very large positive number.
Similar properties hold when x is negative.
Note, however, that x may not be 0. 0 is the only value that must be excluded from the domain.
We will go into this more in Topic 18.
Next Topic: The vocabulary of polynomial functions
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2018 Lawrence Spector
Questions or comments?
E-mail: themathpage@yandex.com
Private tutoring available.