Appendix 2
ODD AND EVEN
NUMBERS
IT IS POSSIBLE TO CLASSIFY natural numbers in many different ways. Square numbers, prime numbers, powers of 10. But the most fundamental classification is odd or even.
The demonstrations in this lesson could easily be done with algebra—that symbolic calculator. But this is arithmetic, and we can deal with numbers themselves.
A natural number is not simply a symbol that obeys formal rules.
![]()
We say that a number is even if it can be "evenly" divided into two equal parts:
![]()
A number is odd if it cannot.
![]()
There is an "odd" 1.
In terms of division, an even number is divisible by 2, but an odd number is not. There is a remainder of 1.
It is easy to see that the sum of two even number is even:
![]()
The sum of two odd numbers is also even.
![]()
Only the sum of an odd number and an even number is odd.
![]()
Square numbers
We call a number a square number when it can take the form of a square.

How is a square number produced?
By adding consecutive odd numbers.
![]()
To the first odd number 1 we add the odd number 3 to produce 4.
![]()
To 4 we add 5 to produce 9.
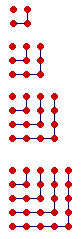
To 9 we add 7 to produce 16.
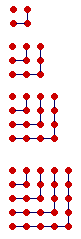
To 16 we add 9 to produce 25.
Every square number is a sum of consecutive odd numbers.
| 1. | ||
| 1 + 3 | = | 4. |
| 1 + 3 + 5 | = | 9. |
| 1 + 3 + 5 + 7 | = | 16. |
| 1 + 3 + 5 + 7 + 9 | = | 25. |
Note the following:
An even square is the sum of an even number of odd numbers.
An odd square is the sum of an odd number of odd numbers.
For, the sum of any two consecutive odd numbers is even.
![]()
Therefore the sum of an odd number of odd numbers will be odd.
As for a square number being a number multiplied by itself, that follows from it being in a square array.

5 × 5 is 5 repeatedly added five times. We see that in the five horizontal rows.
Pythagorean triples
Now, when the odd number that is added to the previous square is itself a square, then
the sum of two square numbers will equal a square number.
16 + 9 = 25.
That is,
32 + 42 = 52.
3-4-5 is called a Pythagorean triple. They are three whole numbers such that the sum of the squares of two of them is equal to the square of the third.
For every odd square, then, there will be a Pythagorean triple.
| 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | |||||||||||||||||
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 | 31 | 33 |
The next odd square is 25. And we see that
144 + 25 = 169.
The Pythagorean triple is 5-12-13.
Because 5-12-13 have no common divisors, they are said to be a primitive triple. So are 3-4-5.
In every primitive triple, two numbers are odd and one is even. In our examples, an odd square was added to an even square to produce an odd square. The sum two even squares producing an even square would not be a primitive triple.
Now the next odd square is 49. What square number will it be added to? What Pythagorean triple will be produced?
To answer, consider that each odd number is 1 more than an even number. Let us call that even number the even part. Thus the even part of 3 is 2. The even part of 5 is 4. And so on.
Each odd number will be added to the square of half of its even part.
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | ||||||||||
| The even part | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | ||||||||||
| Half | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
The even parts are the sequence of even numbers.
The halves are the sequence of the numbers that are squared.
12, 22, 32, 42. And so on.
Beginning with 3, each odd number is added to the previous square.
| 1 + 3 | = | 4. |
| 3 is added to the square of 1. | ||
| 1 + 3 + 5 | = | 9. |
| 5 is added to the square of 2. | ||
| 1 + 3 + 5 + 7 | = | 25. |
| 7 is added to the square of 3. | ||
Each odd number will be added to the square of half of its even part.
As for the odd square 49, which is the square of 7:
49 = 24 + 1 + 24.
49 will be added to the square of 24, producing the square of 25. The Pythagorean triple is 7-24-25.
Problem. The next odd square is 81. What Pythagorean triple will it produce?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
81 = 40 + 1 + 40.
81 will be added to the square of 40.
The Pythagorean triple is 9-40-41..
Division by 4
Odd and even are how we classify numbers upon division by 2. Classifying numbers upon division by 4 leads to interesting results.
Thus a number will either be divisible by 4, or it will have a remainder of 1, or 2, or 3.
11 12 13 14 15 16 17
In other words, a number will either be a multiple of 4, or 1 more than a multiple, or 2 more, or 3 more—which is to say, 1 less.
2 4 6 8 10 12 14 16 18 20
All multiples of 4 are even. A number two more than a multiple of 4 will also be even, because that is the next even number.
1 3 5 7 9 11 13 15 17 19 21
Odd numbers are either 1 more than a multiple of 4 or 1 less, and they alternate. If we count 0 as a multiple of 4 (0 = 0 × 4), then 1 is 1 more than a multiple of 4. 3 is 1 less. 5 is 1 more. 7 is 1 less. And so on.
Which odd numbers will be 1 more, and which will be 1 less?
1 is the 1st odd number. 3 is the 2nd. 5 is the 3rd. And so on.
Each number in an odd position—1st, 3rd, 5th, etc.—will be 1 more than a multiple of 4, which are every 4 numbers beginning with 1:
1, 5, 9, 13, 17, 21, 25, 29, 33, 37, . . .
We will now see that every odd square is in that sequence.
Every odd square is 1 more than a multiple of 4.
For, the sum of any two consecutive odd numbers is a multiple of 4, a sum of 4's.
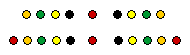
Therefore, an even number of consecutive odd numbers is a multiple of 4.
| 1. | ||
| 1 + 3 | = | 4. |
| 1 + 3 + 5 | = | 9. |
| 1 + 3 + 5 + 7 | = | 16. |
| 1 + 3 + 5 + 7 + 9 | = | 25. |
| 1 + 3 + 5 + 7 + 9 + 11 | = | 36. |
| 1 + 3 + 5 + 7 + 9 + 11 + 13 | = | 49. |
Every even square is a multiple of 4.
An odd square is produced by adding the next odd number. And that odd number is in an odd position—because an odd square is the sum of an odd number of odd numbers.
That odd number is 1 more than a multiple of 4. And a multiple of 4—an even square—plus a number 1 more than a multiple 4, is itself 1 more than a multiple of 4.
Therefore every odd square—
1 9 25 49 81 121 169 225
—is 1 more than a multiple of 4. When that odd number is added, we will have a Pythagorean triple. And the square that is produced is odd. It is 1 more than a multiple of 4.
In other words, in every Pythagorean triple produced in this way:
The sum of two squares is 1 more than a multiple of 4.
| 16 + 9 | = | 25. |
| 144 + 25 | = | 169. |
| 576 + 49 | = | 625. |
| 1600 + 81 | = | 1681. |
Why have we gone to the trouble to show that the sum of two squares is 1 more than a multiple of 4? Because there is another class of numbers for which that is true. Namely, prime numbers that are 1 more than a multiple of 4.
5 13 17 29 37 41 53 57 61 73 89
Every one of those primes is the sum of two squares![]() Every one could be the square drawn on the hypotenuse of a right-triangle. Every one is the sum of two consecutive sums of odd numbers.
Every one could be the square drawn on the hypotenuse of a right-triangle. Every one is the sum of two consecutive sums of odd numbers.
| 5 | = | 4 + 1. |
| 13 | = | 4 + 9. |
| 17 | = | 16 + 1. |
| 29 | = | 4 + 25. |
| 37 | = | 36 + 1. |
| 41 | = | 16 + 25. |
| 53 | = | 4 + 49. |
That is not true for a prime that is 1 less than a multiple of 4; which is the other possibility for an odd prime. It is true only for a prime that is 1 more.
That fact is not difficult to understand. But it is quite difficult to prove. It has been called Fermat's Theorem on the Sum of Two Squares; although the fact has been known since ancient times.
![]()
Introduction | Home | Table of Contents
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
