Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

THE PYTHAGOREAN THEOREM
Book I. Propositions 47 and 48
Pythagoras and the Pythagoreans
PYTHAGORAS was a teacher and philosopher who lived some 250 years before Euclid, in the 6th century B.C. The theorem that bears his name is about an equality of non-congruent areas; namely the squares that are drawn on each side of a right triangle.
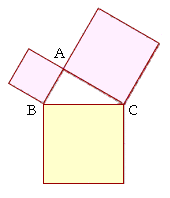
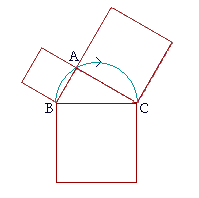
Thus if ABC is a right triangle with the right angle at A, then the square drawn on BC opposite the right angle, is equal to the two squares together drawn on BA, AC.
That is, if it takes one can of paint to paint the square on BC, then it will also take exactly one can to paint the other two squares.
That is how the sides of a right triangle are related -- by the squares drawn on them -- and we can illustrate it with numbers.
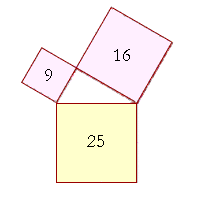
The square drawn on the side opposite the right angle, 25, is equal to the squares on the sides that make the right angle: 9 + 16. Thus a triangle whose sides are 3-4-5 is right-angled.
That and other facts were known to many cultures long before Pythagoras, but credit has gone to him for being the first to prove the theorem. It is the culmination of Euclid's first Book.
PROPOSITION 47. THEOREM
| In a right triangle the square drawn on the side opposite the right angle is equal to the squares drawn on the sides that make the right angle. |
|
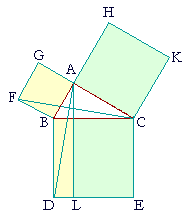
| Let ABC be a right triangle in which CAB is a right angle; then the square drawn on BC is equal to the two squares on BA, AC. |
|
 |
|
| On BC draw the square BDEC, and on BA, AC draw the squares GB, HC; |
(I. 46) |
| through A draw AL parallel to BD or CE; and draw AD and FC. |
|
(The proof now shows that the square GB is equal to the parallelogram BL, and the square HC is equal to the remaining parallelogram CL.
To show that the square GB is equal to the parallelogram BL,
the proof first establishes that triangles FBC, ABD are equal.
Next, the square GB is double triangle FBC because they are on the same base FB and in the same parallels FB, GC; while parallelogram BL
is double triangle ABD. And doubles of equals are equal to one another.)
 |
||
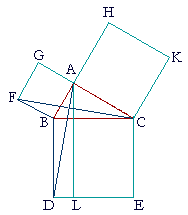
| Then, since each of the angles BAG, BAC is a right angle, GA, CA upon meeting at A make the adjacent angles equal to two right angles; |
||
| therefore GA is in a straight line with CA. | (I. 14) | |
| For the same reason, BA is in a straight line with HA. | ||
| Now, angle FBA is equal to angle DBC because each is a right angle. | ||
| To each of them join angle ABC. | ||
| Therefore the whole angle FBC is equal to the whole angle ABD. | (Axiom 2) | |
| And since FB is equal to BA, and DB to BC, | ||
| the two sides FB, BC are equal to the two sides AB, BD respectively; | ||
| and we proved that angle FBC is equal to angle ABD; | ||
| therefore triangle FBC is equal to triangle ABD. | (S.A.S.) | |
 |
||
| Now the parallelogram BL is double the triangle ABD because they are on the same base BD and in the same parallels BD, AL. |
(I. 41) |
| And the square GB is double the triangle FBC because they are on the same base FB and in the same parallels FB, GC. |
|
| But doubles of equals are equal to one another. | (I. 37, Problem 2.) | |
| Therefore the square GB is equal to the parallelogram BL. | ||
 |
||
| In the same way, by drawing AE, BK, we could show that the square HC is equal to the parallelogram CL. | |
| Therefore the whole square BDEC is equal to the two squares GB, HC. | (Axiom 2) |
| And the square BDEC is drawn on BC, and the squares GB, HC on BA, AC. | |
| Therefore the square drawn on BC is equal to the two squares on BA, AC. | |
| Therefore, in a right triangle etc. Q.E.D. | |
![]()
The side opposite the right angle is called the hypotenuse
("hy-POT'n-yoos"); which literally means stretching under.
The above proof is Euclid's, not Pythagoras's. His proof is believed to have been based on the theory of proportions; Proposition VI. 31.
Now it is also a theorem that if BC is the diameter of a circle
and A any point on the circumference, then angle BAC is always a right angle. (Proposition III. 31.) Therefore if we imagine the point A moving along the circumference, then at each point we will have a right angle. The square on BA will grow larger while the square on AC grows smaller, yet they continually adjust themselves so that together they equal the constant square on BC! That equality of areas is what makes Pythagoras's theorem so remarkable.
Moreover, actually seeing that equality -- feeling it, almost -- rather than just proving it, is the essence of geometry. For however easy or difficult it might be to prove, actually seeing the fact -- that those areas really are equal -- remains elusive. Over the centuries therefore there have been many, many proofs of this famous theorem, each one offering a different insight. For example, see this one.
The converse
The hypothesis of Proposition 47 is that the triangle is right-angled; hence the converse, which is Proposition 48 and the last theorem of Book I, has for its conclusion that the triangle is right-angled. Here is the enunciation.
PROPOSITION 48. THEOREM
| If the square drawn on one side of a triangle is equal to the squares drawn on the other two sides, then the angle contained by those two sides is a right angle. |
![]()
It is this proposition that informs us that if the sides of a triangle are 3-4-5 -- so that the squares on them are 9-16-25 -- then the triangle is right-angled. Whole-number sides such as those are called Pythagorean triples.
For the proof, see Problem 4.
Pythagoras and the Pythagoreans
Pythagoras is remembered as the first to take mathematics seriously in relation to the world order. He taught that geometry and numbers should be studied with reverence because we are entering into knowledge of the Divine. Mathematics is therefore more than just intellectual stimulation, and its relationship to the Universe is more than just coincidence.
Pythagoras was born on the Greek island of Samos. He left to found what we might call a religious sect in the city of Crotona in southern Italy, which was then part of greater Greece. His devotees were called Pythagoreans ("Pi-thag-o-REE-ans"), and many of them, both men and women, lived communally. They had their rituals and dietary laws, and they made important contributions to the medicine and astronomy of their time. They were among the first to teach that the earth is round and that it revolves about the sun.
They also taught the continuity and reincarnation of life; and that through philosophy (literally, love of wisdom) there is purification and thus escape from the cycle of births. Hence they practiced equality between one another, and they showed compassion to all creatures because we are all forms of One.
The Pythagoreans were the first to systematically investigate both arithmetic and geometry. Not
![]() only did they discover many theorems, but they gave an ethical and spiritual significance to each of the figures they drew. As a secret society, it must be said that they were extremely successful. Not a word has survived. Nevertheless, Pythagoras is credited with discovering that the diagonal and side of a square have no common meausre. (See Topic 11 of The Evolution of the Real Numbers.) They considered their doctrine of incommensurables their most esoteric teaching -- one of their members was treated as dead for having even spoken of it to an outsider. The significance they gave to it has never been revealed.
only did they discover many theorems, but they gave an ethical and spiritual significance to each of the figures they drew. As a secret society, it must be said that they were extremely successful. Not a word has survived. Nevertheless, Pythagoras is credited with discovering that the diagonal and side of a square have no common meausre. (See Topic 11 of The Evolution of the Real Numbers.) They considered their doctrine of incommensurables their most esoteric teaching -- one of their members was treated as dead for having even spoken of it to an outsider. The significance they gave to it has never been revealed.
As a scientific researcher, Pythagoras discovered how musical harmonies depend on ratios of whole numbers. He found that we

hear the interval called an octave when the length of a vibrating string is halved, that is to say, when the length of the plucked string is to the whole string in the ratio 1:2 (Fig 1). We hear the interval called a perfect fifth (G above C) when two thirds of a string is plucked (Fig. 2), that is, when the stopped string is to the whole string in the ratio 2:3. And we hear a perfect fourth (F above C) when three fourths of the string is sounded (Fig. 3); and so on, for each interval in the musical scale.
For the Pythagoreans, it was not just that they understood that. They believed that those numerical ratios created the harmonious sounds.
"All things take their form from number." (Not symbols for numbers.) All things are therefore intelligible.
![]()
Please "turn" the page and do some Problems.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com