Lesson 30
WHAT PERCENT?
The Method of Proportions
The first lesson on percent is Lesson 4.
In this Lesson we hope to give the student an understanding rather than just a mechanical method to get an answer.
In Lesson 14 we saw how to use a calculator to solve percent problems. And in Lesson 18 we first introduced the method of proportions. In this Lesson we will see problems that anyone who understands percent can easily do mentally. Arithmetic is and always has been a spoken skill.
To understand how we use the terms Amount and Base, see Lesson 28.
In this Lesson, we will answer the following:
| 1. | Any number is what percent of 100? |
| 5 is ? % of 100. | |
| Any number is that percent of 100. | |
5 is 5% of 100. 12 is 12% of 100. 250 is 250% of 100.
For, a percent is a number of hundredths. 5 is 5 hundredths -- 5% -- of 100. That is the ratio of 5 to 100. For a percent expresses a ratio, a relationship, between two numbers. What ratio has 6 to 12? 6 is half of 12, or, in the language of percent, 6 is 50% of 12.
When the percent is less than or equal to 100%, then we can say "out of" 100. 25% is 25 out of 100. But 250% cannot mean 250 out of 100 -- that makes no sense. It means 250 for each 100, which is two and a half times. (Lesson 16.)
Example 1. $42.10 is what percent of $42.10?
Answer. 100%. 100% is all.
The method of proportions
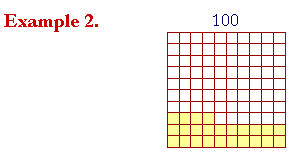
24 out of 100 is 24%. Equivalently, 24 is 24% of 100.
But what percent is 24 out of 200? 24 is what percent of 200?
Answer. Percent is how many out of 100. But if there are 24 out of 200 --
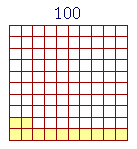

-- then out of each 100 there are half as many: 12.
24 is 12% of 200.
Since percents are ratios, then as a proportion problem, we must find the missing term:
24 out of 200 is equal to ____ out of 100?
When we say "24 out of 200," then the Base -- the number that follows "of" -- is 200. But with percent, the Base must be 100. What must we do then to 200 to make it 100? We must take half of it or, equivalently, divide it by 2. Therefore we must also divide 24 by 2.
24 out of 200 is equal to 12 out of 100.
But 12 out of 100 is 12%. Therefore, 24 out of 200 is also 12%.
Example 3. What percent is 24 out of 50? Equivalently, 24 is what percent of 50?
Answer. Again, percent is how many out of 100. But if there are 24 out of 50 --
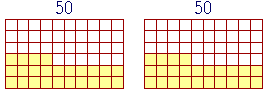
-- then out of 100, there are two 24's: 48.
24 is 48% of 50.
Proportionally,
24 out of 50 is equal to 48 out of 100.
Now without even having to write that, the student should see that to go from base 50 to base 100, we have to multiply by 2. Therefore we must multiply 24 by 2, also.
An all too common method these days is to make this an algebra problem.
| 24 50 |
= | x 100 |
The student is taught to cross-multiply and solve for x. That is a method for someone who does not understand percent. Whoever does understand percent will either do such a problem mentally, or, if that is too difficult, with a calculator: Percent = Amount ÷ Base.
| 2. | How do we find the Percent by the method of proportions? |
| Solve the proportion in which 100 is the fourth term, and the Amount and Base are the first and second. | |
| "The Amount is to the Base as what number is to 100?" | |
The Base will always follow "of." Therefore to find what percent one number is of another, we must make the Base 100.
(But see below.)
Example 4. 3 out of 10 students got A. What percent got A?
That is, 3 is what percent of 10? Those questions mean the same. In each one, the base 10 follows "of."
Solution. On multiplying both numbers by 10,
3 out of 10 is equal to 30 out of 100.
30% got A.
Example 5. In a class of 25 students, 11 studied French. What percent studied French?
Solution. The student should understand that this means,
11 out of 25 studied French.
To make the base 100, we must multiply 25 by 4. Therefore we must also multiply 11 by 4:
11 is to 25 as 44 is to 100.
44% studied French.
While it is possible to do this problem by writing the
proper fraction ![]() , and then solving this proportion:
, and then solving this proportion:
| 11 25 |
= | ? 100 |
, |
the student should not have to write that. On seeing, or even hearing, the phrase "11 out of 25," the student should understand that we must multiply both 11 and 25 by 4.
Understanding that is skill in arithmetic.
Example 6. In a class of 200 students, 11 studied French. What percent studied French?
Solution. In this case, to make 200 into 100, we must divide by 2, or take half. Therefore we must also take half of 11, which is 5½.
5½% studied French.
We see that to solve a proportion:
We must divide both terms by the same number,
or we must multiply both terms by the same number.
Example 7. What percent of 400 is 33?
Solution. 400 is the Base; it follows "of." To make it 100, we must divide by 4. Therefore we must also divide 33 by 4.
| 33 4 |
= | 8¼. |
"4 goes into 33 eight (8) times (32) with 1 left over."
33 is 8¼% of 400.
Example 8. 1000 people voted in the recent election, and 763 voted for Jones. What percent voted for Jones?
Solution. 763 out of 1000 voted for Jones. To make the Base 100, we must divide by 10. To divide 763 by 10, simply separate one decimal digit.
763 ÷ 10 = 76.3
76.3% voted for Jones.
Example 9. What percent of 500 is 132?
Solution. 132 is to 500 as 264 is to 1000 as 26.4 is to 100.
132 is 26.4% of 500.
Example 10. 7 out of 12 people voted Yes. Approximately what percent voted Yes?
Solution. What number times 12 is close to 100?
8 × 12 = 96. 8 × 7 = 56. Therefore approximately 56% voted Yes.
The ratio of the Amount to the Base
Example 11. 8 is what percent of 40?
Answer. That question means the same as, "8 has what ratio to 40?" For percents are ratios.
Now, 8 is the fifth part of 40. And since 20 is the fifth part of 100:
8 is 20% of 40.
To master the subject of percent, the student should master Problem 1 of Lesson 28.
Example 12. What percent of 8 is 40?
Answer. Here, 8 is the Base -- it follows "of." It is possible to see that better if we express the question in standard form:
40 is what percent of 8?
Now, 40 is five times 8. The percent will have that same ratio to 100%. Five times 100% is 500%.
40 is 500% of 8.
Example 13. In a class of 28 students, 7 got A. What percent of the class got A?
Answer. The question is: 7 is what percent of 28?
It is not obvious how to make 28 into 100. But 7 is the fourth part, or a quarter, of 28. And as a percent, a quarter of a number is 25%.
7 is 25% of 28.
Example 14. 12 is what percent of 18?
Answer. 12 has what ratio to 18? They have a common divisor 6.
"6 goes into 12 two times and into 18 three times."
12 is to 18 as 2 is to 3 --
12 is two thirds of 18.
Each number says its name.
As a percent, 66![]() % means two thirds.
% means two thirds.
12 is 66![]() % of 18.
% of 18.
Example 15. What percent of 35 is 14?
Answer. In standard form,
14 is what percent of 35?
They have a common divisor 7. Therefore, on dividing each term by 7:
14 is to 35 as 2 is to 5.
2 is two fifths of 5. Two fifths of 100% is 40%. (One fifth is 20%.) Therefore,
14 is 40% of 35.
Example 16. 20 is what percent of 8?
Answer. 20 is made up to two 8's -- 16 -- plus 4, which is half of 8. 20 is two and a half times 8.
20 is 250% of 8.
Example 17. Clearing of decimals. .8 is what percent of 4?
Answer. To solve any percent problem, the numbers must be whole numbers. Therefore, make the numbers whole numbers by multiplying by 10:
.8 is to 4 as 8 is to 40.
Now, 8 is the fifth part of 40. That tells us,
.8 is 20% of 4.
Example 18. What percent of 75 is 21?
Solution 1. In standard form,
21 is what percent of 75?
They have a common divisor 3. That tells us that each number has a third part. And on taking a third of each one:
21 is to 75 as 7 is to 25.
We can now change 25 to 100 by multiplying by 4. Therefore, on also multiplying 7 by 4:
21 is 28% of 75.
| Solution 2. | 21 75 |
= | ? 100 |
What number times 75 will produce 100? In other words, What ratio has 100 to 75?
Answer:
100 is one and a third times 75.
One times 75 is 75. One third of 75 is 25. 75 plus 25 is 100.
Therefore, one and a third times 21 is 21 + 7 = 28.
21 is 28% of 75.
Example 19. Same digits. $2.50 is what percent of $250?
Answer. The digits are the same: 2, 5, 0; but $2.50 has two decimal digits. It is $250 divided by 100:
$2.50 = $250 ÷ 100.
Therefore,
$2.50 is 1% of $250.
Compare Lesson 15, Examples 5 and 6.
Example 20. $84.50 is what percent of $845?
Answer. 10%. $84.50 = $845 ÷ 10.
Which is how to take 10% of a number.
Summary
To find what percent one number is of another:
Multiply or divide both terms so that the Base becomes 100.
9 is what percent of 20?
It is easy to make 20 into 100 by multiplying it by 5. And since 5 times 9 is 45,
9 is 45% of 20.
When it is not obvious how to make the base 100: Look directly at the ratio of the Amount to the Base.
7 is what percent of 28?
Since 7 is one quarter of 28, then
7 is 25% of 28.
Example 21. 742 people were surveyed, and 213 responded No. What percent responded No?
Solution. 213 is what percent of 742? Use your calculator![]()
At this point, please "turn" the page and do some Problems.
or
Continue on to Section 2: A general method for finding the Percent.
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
