33
THE EQUATION AND GRAPH
OF A STRAIGHT LINE
Solutions to an equation of the first degree
The graph of a first degree equation
The x- and y-intercepts of a graph
y = 2x + 6.
That is called an equation of the first degree. It is called that because the highest exponent is 1.
A solution to that equation will be any values of x and y that will make the equation—that statement—true. For example, the ordered pair (1, 8) is a solution—because if we let x = 1 and y = 8, the equation is true:
8 = 2 · 1 + 6 = 2 + 6.
In fact, to find a solution, simply let x have any value you please. The equation will then determine the value of y.
For example, if we let x = 0, then
y = 2 · 0 + 6 = 0 + 6 = 6.
The pair (0, 6) solves that equation.
If we choose x = 3, then
y = 2 · 3 + 6 = 6 + 6 = 12.
The pair (3, 12) also solves that equation. In fact, when there are two unknowns, x and y, but only one equation that relates them, then there is no limit to the number of solutions.
Since we typically first choose the value of x, we call x the independent variable. y will be the dependent variable, because its value will depend on the value we have chosen for x.
Problem 1. Find three solutions to the first degree equation y = x + 5.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
For example: (0, 5), (1, 6), (2, 7).
Problem 2. Which of the following ordered pairs solve this equation:
y = 3x − 4 ?
(0, −4) (1, 2) (1, −1) (2, −3)
(0, −4) and (1, −1). Because when x and y have those values, the equation is true.
The graph of a first degree equation
Consider the equation
y = 2x + 1.
Since there are two variables, x and y, then will it be possible, on the x-y plane, to draw a "picture" of all the solutions to that equation?
First, to find a few solutions, complete this table. That is, calculate the value of y that corresponds to each value of x:
| x | y = 2x + 1 |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| −1 | −1 |
Now plot those ordered pairs as coördinates on the plane:
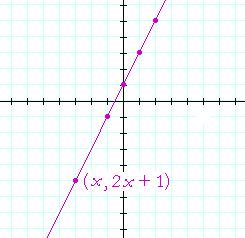
We see that all those solutions lie on a straight line. In fact, every pair (x, y) that solves that equation will be the coördinates of a point on that line. On that line, every coördinate pair is
(x, 2x + 1).
y = 2x + 1.
That line, therefore, is called the graph of the equation y = 2x + 1. And y = 2x + 1 is called the equation of that line.
The graph of an equation, in other words, is the graph of its solutions. It is the picture of those values of (x, y) that make the equation -- that statement -- true.
Every first degree equation -- where 1 is the highest exponent -- has as its graph a straight line. (We prove that in Topics in Precalculus .)
For that reason, an equation of the first degree is called a linear equation.
Problem 3.
a) An equation of the form y = ax + b has what graph?
A straight line. This is a linear equation.
b) An equation of the form Ax + By + C = 0 has what graph?
A straight line. This is a linear equation. The capital letters are a convention for indicating integer coefficients.
Problem 4. What characterizes a linear equation?
1 is the highest exponent.
Problem 5. Which of the following are linear equations?
| a) y = 4x − 5 | b) 2x − 3y + 8 = 0 | c) y = x² − 2x + 1 | ||
| d) 3x + 1 = 0 | e) y = 6x + x3 | f) y = 2 | ||
a), b), d), f).
Problem 6.
| a) | Name the coördinates of any three points on the line whose equation is |
y = 2x − 1.
| (Choose any number for x; the equation will then determine the value of y.) |
For example, (0 −1), (1, 1), (−1, −3).
Problem 7.
a) Which of these ordered pairs solves the equation y = 5x − 6 ?
(You have to test each pair.)
(1, −2) (1, −1) (2, 3) (2, 4)
(1, −1) and (2, 4)
b) Which of those are points on the graph of y = 5x − 6 ?
(1, −1) and (2, 4)
Problem 8. True or false?
a) (−2, −3) is on the line whose equation is x + y = 5.
False.
b) (2, 3) is on the line whose equation is x + y = 5.
True.
Constants versus variables
A constant is a symbol whose value does not change. The symbols 2, 5, ![]() ,
, ![]() are constants.
are constants.
The beginning letters of the alphabet a, b, c, are typically used as arbitrary constants, which could be any specific numbers; while the letters x, y, z, are typically used to denote variables. For example, if we write
y = ax² + bx + c,
we mean that a, b, c are numbers, and that x and y are variables.
Problem 9. The arbitrary constants a and b. Each of the following has the form y = ax + b. What number is a and what number is b?
| a) y = 2x + 3. | a = 2, b = 3. | b) y = x − 4. | a = 1, b = −4. | |
| c) y = −x + 1. | a = −1, b = 1. | d) y = 5x. | a = 5, b = 0. | |
| e) y = −2. | a = 0, b = −2. | f) y = −4x − 5. | a = −4, b = −5. | |
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
