11
INEQUALITIES
THIS SIGN < means is less than.. This sign > means is greater than. In each case, the sign opens towards the larger number.
For example, 2 < 5 ("2 is less than 5"). Equivalently, 5 > 2 ("5 is greater than 2").
These are the two senses of an inequality: < and > .
The number line
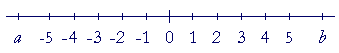
On the number line, a < b means: a falls to the left of b.
| 2 | < | 5 |
| −1 | < | 2 |
| −4 | < | −1 |
| 1 | > | −4 |
Problem 1. Between each pair, place the correct sign of inequality.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| 3 | < | 7 | 8 | > | 5 | −2 | < | 1 | −6 | < | −2 | |||
| −3 | > | −9 | −10 | > | −12 | 0 | > | −9 | −6 | < | 0 | |||
"Or" versus "and"
The following is called a compound inequality:
x > 1 and x ≤ 5.
It is a compound sentence whose conjunction is "and." It says that x takes on values that are greater than 1 and less than or equal to 5.
![]()
It is within that interval that x takes its values. The endpoint 1 is not included. x is definitely greater than 1; we indicate that by placing a parenthesis "(". The endpoint 5 is included; we indicate that by placing a bracket "]".
Now consider this compound inequaltiy:
x < 1 or x > 5.

Here, the values of x are either less than 1 or greater than 5.
It should be clear that x could not be a number that is less than 1 and greater than 5. There is no such number.
So, when the conjunction is and,
x > 1 and x ≤ 5.
![]()
the values of x fall inside a certain interval. But when the conjunction is or,
x < 1 or x > 5.

the values of x fall outside an interval.
Problem 2. Graph these compound inequalities.
a) x < −1 or x ≥ 3.
![]()
b) x ≥ −1 and x < 3.
![]()
A continued inequality
a < x < b
That is called a continued inequality. It means
a < x and x < b.
![]()
A continued inequality always implies the conjunction and. The sense is always < or ≤.
The continued inequality means:
x falls in the interval between a and b.
"a < x < b" illustrates that.
Note: When neither end point is included, as in the example above, we call that an open interval. When both end points are included --
![]()
-- we call that a closed interval. (Otherwise, like the proverbial glass, the interval is half-open, or half-closed.)
Problem 3. Write as a continued inequality.
a) x > −3 and x < 1.
−3 < x < 1.
b) Graph that continued inequality.
![]()
Problem 4. 0 < x < 6. Write that continued inequality as a compound inequality.
x > 0 and x < 6.
Problem 5. Write as a continued inequality:
x < 1 or x > 5.
Not possible! The conjunction must be and.
Problem 6. Write in symbols.
a) x is a positive number. x > 0
b) x is a negative number. x < 0
c) x is a non-negative. x ≥ 0. "x is greater than or equal to 0."
Some theorems of inequalities
A theorem is a statment that can be proved. To prove a statment whose predicate is "is greater than," we must have a definition of "is greater than." We shall adopt the following. We shall define "a is greater than b" to mean: a − b is positive. Algebraically:
a > b if and only if a − b > 0.
On the basis of this definition, we can prove various theorems about inequalities.
Theorem 1. We may add the same number to both sides of an inequality, and the sense will not change.
| If | |||
| a | > | b, | |
| then | |||
| a + c | > | b + c. | |
Note: If c is a negative number, then the theorem implies that we may subtract the same number from both sides. Just as with equalites, any theorem of addition is also true for subtraction.
It follows from this Theorem, that we may transpose.
| x + d | > | e | |
| implies | x | > | e − d. |
We could prove that by adding −d to both sides.
We can prove Theorem 1 as follows:
| a | > | b |
| means | ||
| a − b | > | 0. |
| Therefore, upon adding and subtracting c : | ||
| a − b + c − c | > | 0 |
| (a + c) − (b + c) | > | 0 (Lesson 7) |
| Therefore, | ||
| a + c | > | b + c. |
Which is what we wanted to prove.
Note that any theorem of inequality is true for an inequality of the opposite sense. For, we could write: b < a implies b + c < a + c.
Theorem 2. We may multiply both sides of an inequality by the same positive number, and the sense will not change.
| If | |||
| a | > | b, and c > 0, | |
| then | |||
| ca | > | cb. | |
For example:
| 4 | > | −5. | |
| If we now multiply both sides by 3, for example, then | |||
| 12 | > | −15. | |
The sense does not change.
The proof is similar to that of Theorem 1. Simply apply the Rule of Signs.
| a | > | b | |
| implies | |||
| a − b | > | 0. | |
| Therefore, if c is positive, then | |||
| c(a − b) | > | 0 | |
| ca − cb | > | 0. | |
| This means | |||
| ca | > | cb. | |
This theorem also allows us to divide both sides by the same positive number, because division is multiplication by the reciprocal.
Theorem 3. If we multiply both sides of an inequality by the same negative number, the sense of the inequality changes.
| If | |||
| a | > | b, and c < 0, | |
| then | |||
| ca | < | cb. | |
Here is an example:
| −2 | < | 5. | |
| If we now multiply both sides by −3, say, then | |||
| 6 | > | −15. | |
The sense changes.
(As in Theorem 2, this one also implies that when we divide both sides by a negative number, the sense changes, because division is multiplication by the reciprocal.)
Proof:
| a | > | b | |
| implies | |||
| a − b | > | 0. | |
| Therefore, if c is negative, then according to the Rule of Signs: | |||
| c(a − b) | < | 0 | |
| ca − cb | < | 0. | |
| This means | |||
| ca | < | cb. | |
Theorem 4. If we change the signs on both sides of an inequality,
then the sense of the inequaltiy will change.
| If | |||
| a | > | b, | |
| then | |||
| −a | < | −b. | |

We can see that on the number line.
We could prove it simply by transposing −a and −b.
For example, since
| −1 | < | 2, | |
| then on changing the signs on both sides: | |||
| 1 | > | −2. | |
We may think of Theorem 3 as an instance of Theorem 4, because when we multiply or divide both sides by the same negative number, the signs on each side necessarily change.
Theorem 5. If a, b are both positive or both negative, then on taking reciprocals, the sense of the inequality changes.
| If | ||||
| a | > | b, | ||
| then | ||||
| 1 a |
< | 1 b |
. | |
We can prove that by dividing both sides by ab (which, since a and b have the same sign, will be positive) -- but that will depend on knowing how to reduce fractions.
In any event, since
| 2 | < | 5, | |||
| then | |||||
| 1 2 |
> | 1 5 |
|||
Thus the sense of an inequality changes in only two cases.
1) We change the signs on both sides (Theorem 4); equivalently, multiply both sides by negative number (Theorem 3).
2) We take reciprocals. (Theorem 5.)
| Problem 7. | 1 < | a b |
< x. |
Write the continued inequality that results if
| a) you take reciprocals. | 1 > | b a |
> | 1 x |
| b) you then change all the signs. | −1 < − | b a |
< − | 1 x |
| c) you then add 1 to every term. | 0 | < 1 − | b a |
< 1 − | 1 x |
Problem 8. Use Theorem 2 to prove: If a is a positive number less than 1, then a2 is less than a.
For example, (½)2 = ¼, which is less than ½.
| a | < | 1 | |
| implies | a · a | < | 1 · a |
| That is, | a2 | < | a. |
Problem 9. −a > 0. How is that possible?
a is not a number. It is a variable. It takes values which are numbers. To find the values of a such that −a > 0, apply Theorem 4, and change the signs on both sides. But then we must change the sense.
| −a | > | 0 | |
| implies | a | < | −0. |
That is, since −0 = 0,
a < 0.
a must be a negative number. For example, if a = −5, then −a = −(−5) = +5, that is, −a is a positive number.
Solving inequalities
A linear inequality has this standard form:
ax + b < c.
When a is positive, then solving it is identical to solving an equation:
| ax | < | c − b |
| x | < | c − b a |
As with equations, the inequality is "solved" when positive x is isolated on the left. (The above steps follow from Theorems 1 and 2.)
The only difference between solving an inequality and solving an equation, is the following:
When we multiply or divide by a negative number,
the sense must change. (Theorem 3.)
Equivalently, when the signs on both sides change, then the sense also must change (Theorem 4).
Example 1.
| −2x + 5 | < | 11 |
| −2x | < | 6 |
| x | > | −3. |
On going to the last line, the signs on both sides changed. Therefore, the sense also changes.
The signs changed, of course, because we divided both sides by negative 2.
Alternatively, we could immediately make 2x positive -- by changing all the signs on both sides. But then we must also change the sense.
−2x + 5 < 11 implies 2x − 5 > −11,
and so on.
Problem 10. Solve each inequality for x. Write a logical sequence of statements.
| a) 5x + 3 | < | 38 | b) 5x − 3 | < | 12 | |
| 5x | < | 35 | 5x | < | 15 | |
| x | < | 7 | x | < | 3 | |
| c) −2x + 7 | < | 19 | d) −2x − 1 | < | −9 | |
| −2x | < | 12 | −2x | < | −8 | |
| x | > | −6 | x | > | 4 | |
| e) −3x | < | x − 8 | f) 4x − 7 | < | 11x + 7 | |
| −3x − x | < | −8 | 4x − 11x | < | 7 + 7 | |
| −4x | < | −8 | −7x | < | 14 | |
| x | > | 2 | x | > | −2 | |
Problem 11. In each of the following, what can you conclude about the signs of a and b?
a) ab > 0
a and b must have the same signs.
Formally,
a > 0 and b > 0, or a < 0 and b < 0.
Lesson 4: The Rule of Signs.
b) ab < 0
a and b must have opposite signs.
c) ab = 0
Either a = 0 or b = 0.
| d) | a b |
> 0 |
Same as a). a, b ≠ 0.
| e) | a b |
< 0 |
Same as b). a, b ≠ 0.
| f) | a b |
= 0 |
The numerator must be 0. a = 0.
Example 2. Solve this inequality for x :
| x − 3 x + 5 |
> 0. |
Solution. According to d) above, the numerator and denominator must
have the same sign. Therefore, either
1) x − 3 > 0 and x + 5 > 0,
or
2) x − 3 < 0 and x + 5 < 0.
Now, 1) implies
x > 3 and x > −5.
Which numbers are these that are both greater than 3 and greater than −5?
Clearly, any number greater than 3 will also be greater than −5. Therefore, 1) has the solution
x > 3.
Next, 2) implies
x < 3 and x < −5.
Which numbers are these that are both less than 3 and less than −5?
Clearly, any number less than −5 will also be less than 3. Therefore, 2) has the solution
x < −5.
The solution, therefore, is
x < −5 or x > 3.
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
