12
ABSOLUTE VALUE
The geometrical meaning of |x − a|
THIS SYMBOL |x| denotes the absolute value of x, which is the number without its sign. |+3| = 3. |−3| = 3. We could say that the absolute value of a number is its purely arithmetical value.
Here is the algebraic definition of |x|:
If x ≥ 0, then |x| = x;
if x < 0, then |x| = −x.
That is, if x is non-negative: |3|, then the absolute value is the number itself.
If x is negative: |−3|, then the absolute value is its negative; that makes the absolute value positive.
Geometrically, |x| is the distance of x from 0.
![]()
Both 3 and −3 are a distance of 3 units from 0. |3| = |−3| = 3. Distance, in mathematics, is never negative.
Problem 1. Evaluate the following.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | |6| = 6 | b) | |−6| = 6 | c) | |0| = 0 | d) | |2 − 7| = 5 | |||
| e) | |8| + |−4| = 8 + 4 = 12 | f) | |−3| − |−2| = 3 − 2 = 1 | |||||||
| g) | 1 − |−1| = 1 − 1 = 0 | h) | −8 + |−7| = −8 + 7 = −1 | |||||||
| i) | −4 |−4| |
= | −4 4 |
= −1 | j) (−4)|−4|= (−4)· 4 = −16 |
Problem 2. Explain the following rules.
a) |−x| = |x|.
Both −x and x are the same distance from 0.
b) |b − a| = |a − b|
b − a is the negative of a − b.
Therefore, according to part a), they are equal.
c) |x|² = x²
We may remove the absolute value bars because the left-hand side is never negative, and neither is the right-hand side.
Absolute value equations
|a| = 5.
What values could a have?
a could be either 5 or −5. For if we replace a with either of those, the statement -- the equation -- will be true.
And so any equation that looks like this --
|a| = b
-- has the two solutions
a = b, or a = −b.
Whatever appears within the vertical bars -- a in this example -- we call the argument of the absolute value. Either the argument will equal b, or it will equal −b.
Example 1. Solve for x:
|x − 2| = 8.
Solution. x − 2 is the argument. Either that argument will equal 8 or it will equal −8.
x − 2 = 8, or x − 2 = −8.
We must solve these two equations. The first implies
x = 8 + 2 = 10.
The second implies
x = −8 + 2 = −6.
These are the two solutions: x = 10 or −6.
Problem 3.
a) An absolute value equation has how many solutions? Two.
b) Write them for this equation: |x| = 4.
x = 4, or x = −4.
Problem 4. Solve for x.
|x + 5| = 4.
Solve these two equations:
| x + 5 | = | 4 | x + 5 | = | −4 | ||
| x | = | 4 − 5 | x | = | −4 − 5 | ||
| x | = | −1 | or | x | = | −9 | |
Problem 5. Solve for x.
|1 − x| = 7.
| 1 − x | = | 7 | 1 − x | = | −7 | ||
| −x | = | 7 − 1 | −x | = | −7 − 1 | ||
| −x | = | 6 | −x | = | −8 | ||
| x | = | −6 | or | x | = | 8. | |
Problem 6. Solve for x.
|2x + 5| = 9.
| 2x + 5 | = | 9 | 2x + 5 | = | −9 | ||
| 2x | = | 9 − 5 | 2x | = | −9 − 5 | ||
| 2x | = | 4 | 2x | = | −14 | ||
| x | = | 2 | or | x | = | −7. | |
Absolute value inequalities
There are two forms of absolute value inequalities. One with less than, |a|< b, and the other with greater than, |a|> b. They are solved differently. Here is the first case.
Example 2. Absolute value less than.
|a| < 3.
For that inequaltiy to be true, what values could a have?
Geometrically, a is less than 3 units from 0.
![]()
Therefore,
−3 < a < 3.
This is the solution. The inequality will be true if a has any value between −3 and 3.
In general, if an inequality looks like this --
|a| < b.
-- then the solution will look like this:
−b < a < b
for any argument a.
Example 3. For which values of x will this inequality be true?
|2x − 1| < 5.
Solution. The argument, 2x − 1, will fall between −5 and 5:
−5 < 2x − 1 < 5.
We must isolate x. First, add 1 to each term of the inequality:
−5 + 1 < 2x < 5 + 1
−4 < 2x < 6.
Now divide each term by 2:
−2 < x < 3.
The inequality will be true for any value of x in that interval.
Problem 7. Solve this inequality for x :
|x + 2| < 7.
−7 < x + 2 < 7.
Subtract 2 from each term:
−7 − 2 < x < 7 − 2
−9 < x < 5.
Problem 8. Solve this inequality for x :
|3x − 5| < 10.
−10 < 3x − 5 < 10.
Add 5 to each term:
−5 < 3x < 15.
Divide each term by 3:
| − | 5 3 |
< x < 5. |
Problem 9. Solve this inequality for x :
|1 − 2x| < 9.
−9 < 1 − 2x < 9.
Subtract 1 from each term:
−10 < −2x < 8.
Divide each term by −2. The sense will change.
5 > x > −4.
That is,
−4 < x < 5.
Example 4. Absolute value greater than.
|a| > 3.
For which values of a will this be true?

Geometrically,
a > 3 or a < −3.
This is the form of the solution, for any argument a:
If
|a| > b (and b > 0),
then
a > b or a < −b.
Problem 10. Solve for x :
|x| > 5.
x > 5 or x < −5.
Problem 11. For which values of x will this be true?
|x + 2| > 7.
x + 2 > 7, or x + 2 < −7.
The first equation implies x > 5. The second, x < −9.
Problem 12. Solve for x :
|2x + 5| > 9.
2x + 5 > 9, or 2x + 5 < −9.
Solve those two equations:
| 2x | > | 4 | 2x | < | −14 | ||
| x | > | 2 | or | x | < | −7 | |
Problem 13. Solve for x :
|1 − 2x| > 9.
1 − 2x > 9, or 1 − 2x < −9.
Solve those two equations. On finally dividing by −2,
the senses will change.
| −2x | > | 8 | −2x | < | −10 | ||
| x | < | −4 | or | x | > | 5. | |
The geometrical meaning of |x − a|

Geometrically, |x − a| is the distance of x from a.
|x − 2| means the distance of x from 2. And so if we write
|x − 2| = 4
we mean that x is 4 units aways from 2.
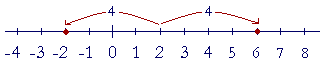
x therefore is equal either to −2 or 6.
On the other hand, if we write
|x − 2| < 4
we mean x is less than 4 units away from 2.
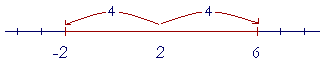
This means that x could have any value in the open interval between −2 and 6.
Problem 14. What is the geometric meaning of |x + a|?
The distance of x from −a. For, |x + a| = |x −(−a)|.
|x + 1|, then, means the distance of x from −1. For example, if
|x + 1| = 2,
then x is 2 units away from −1.
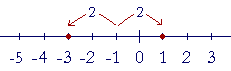
x = −3, or x = 1.
Problem 15. What is the geometrical meaning of each of the following? And therefore what values has x?
a) |x| = 2
x is 2 units away from 0. For, |x| = |x − 0|. x therefore is equal to 2 or −2.
b) |x − 3| = 1
x is 1 unit away from 3. x therefore is equal to 2 or 4.
c) |x + 3| = 1
x is 1 unit away from −3. x therefore is equal to −4 or −2.
d) |x − 5| ≤ 2
x is less than or equal to 2 units away from 5. x therefore may take any value in the closed interval between 3 and 7.
e) |x + 5| ≤ 2
x is less than or equal to 2 units away from −5. x therefore may take any value in the closed interval between −7 and −3.
Problem 16. |x − 5| < d. State the geometrical meaning of that, and illustrate it on the number line.
x falls within d units of 5.
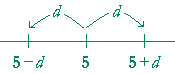
x therefore falls in the interval between 5 − d and 5 + d.
5 − d < x < 5 + d
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
