Perfect square trinomials
Lesson 18, Level 2
Problem 7. Without multiplying out
a) explain why (1 − x)2 = (x − 1)2.
Because (1 − x) is the negative of (x − 1). And (−a)2 = a2 for any quantity a.
b) explain why (1 − x)3 = −(x − 1)3.
(−a)3 = −a3 for any quantity a.
*
The following problem shows how we can go from what we know to what we do not know.
Problem 8. The square of a trinomial. Use your knowledge of
(a + b)2 to multiply out (a + b + c)2.
[Hint: Treat ![]() as a binomial with
as a binomial with ![]() as the first term.]
as the first term.]
| ( |
= | (a + b)2 + 2(a + b)c + c2 |
| = | a2 + 2ab + b2 + 2ac + 2bc + c2 | |
| = | a2 + b2 + c2 + 2ab + 2ac + 2bc | |
We see that that square of a trinomial is equal to the sum of the squares of each term, plus twice the product of all combinations of the terms.
Problem 9. Can you generalize the result of the previous problem? Can you immediately write down the square of (a + b + c + d)?
| (a + b + c + d)2 = | a2 | + b2 + c2 + d2 |
| + 2ab + 2ac + 2ad + 2bc + 2bd + 2cd | ||
Completing the square
x2 + 8x + _?_ = (x + _?_)2
When the coefficient of x2 is 1, as in this case, then to make the quadratic on the left a perfect square trinomial, we must add a square number. What square number must we add?
We must add the square of half of coefficient of x. The trinomial will then be the square of (x + half-that-coefficient).
x2 + 8x + 16 = (x + 4)2
We add the square of half the coefficient of x, because when we expand (x + 4)2, the coefficient of x will be twice that number.
| a) How do we indicate half of any number b? | b 2 |
| b) How do we indicate half of any fraction | p q |
? | p 2q |
(Skill in Arithmetic, Lesson 27, Question 4.)
Example 7. Complete the square:
x2 − 7x + ? = (x − ?)2
Solution. We will add the square of half of 7, which we write as ![]() .
.
| x2 − 7x + | 49 4 |
= | (x − | 7 2 |
)2 |
And since the middle term of the trinomial has a minus sign, then the binomial also must have a minus sign.
Problem 11. Complete the square. The trinomial is then the square of what binomial?
a) x2 + 4x + ? x2 + 4x + 4 = (x + 2)2
b) x2 − 2x + ? x2 − 2x + 1 = (x − 1)2
c) x2 + 6x + ? x2 + 6x + 9 = (x + 3)2
d) x2 − 10x + ? x2 − 10x + 25 = (x − 5)2
e) x2 + 20x + ? x2 + 20x + 100 = (x + 10)2
| f) x2 + 5x + ? x2 + 5x + | 25 4 |
= (x + | 5 2 |
)2 |
| g) x2 − 9x + ? x2 − 9x + | 81 4 |
= (x − | 9 2 |
)2 |
| h) x2 + bx + ? x2 + bx + | b2 4 |
= (x + | b 2 |
)2 |
| i) x2 + | b a |
x + ? | x2 + | b a |
x + | b2 4a2 |
= (x + | b 2a |
)2 |
In Lesson 37 we will see how to solve a quadratic equation by completing the square.
Geometrical algebra
Here is a square whose side is a + b.
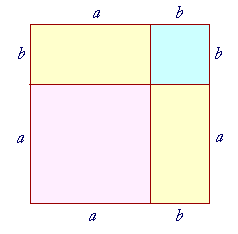
It is composed of a square whose side is a, a square whose side is b, and two rectangles ab. That is,
(a + b)2 = a2 + 2ab + b2.
Now, here is how to complete a rectangle to make it a square![]()
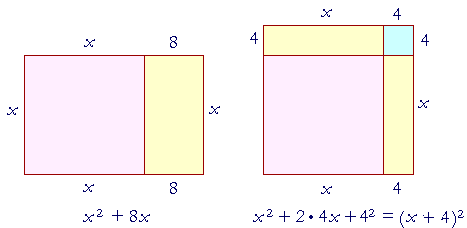
The rectangle on the left is composed of a square whose side is x, and a rectangle 8x. We will now add a square to it and make it a perfect
square. How? By taking half of the rectangle and placing it on top of the square. The figure to complete the square is the square of half the side of the rectangle![]()
Next Lesson: The difference of two squares
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com