Radicals - Rational and irrational numbers: Level 2
The definition of the square root radical
Example 4. Solve for x:
| (x + 3)² | = | 5. | |
| Solution. All equations fall into certain forms, and this one has the same form as Example 3: |
|||
| z² | = | a. | |
| If an equation looks like that, then the solution will look like this: | |||
| z | = | ± |
|
In other words, if we call z the argument of the equation z² = a, then in the solution, the argument is on the left. The argument is whatever was squared.
In this equation --
| (x + 3)² | = | 5, | |
| -- the argument is x + 3. Therefore, | |||
| x + 3 | = | ± |
|
| x | = | −3 ± |
|
Problem 8. Solve for x.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | (x − 1)² | = | 2 | b) | (x + 5)² | = | 6 | |
| x − 1 | = | ± |
x + 5 | = | ± |
|||
| x | = | 1 ± |
x | = | −5 ± |
| c) | (x − p)² | = | q + r |
| x − p | = | ± |
|
| x | = | p ± |
|
The definition of the square root radical
The square root of a is that number which, when squared, produces a.
![]()
A square root radical multiplied by itself
produces the radicand.
That formal rule is the implicit definition of the symbol ![]() .
.
| Example 5. | = | 2. | |
| (3a | = | 3²a²( |
|
| = | 9a² · 10 | ||
| = | 90a². | ||
Problem 9. Evaluate the following.
| a) | b) | ( |
|||||
| c) | ( |
d) | |||||
| e) | (5 |
f) | (a4 |
||||
Example 6. Multiply out ![]()
![]() (
(![]() +
+ ![]() ). That is, distribute
). That is, distribute ![]()
![]() .
.
| Solution. | = | ||
| = | 2 |
||
Problem 10. Following the previous Example, multiply out
![]()
![]() (
(![]() +
+ ![]() ).
).
| = | ||
| = | ||
Rationalizing a denominator
Rationalizing a denominator is a simple technique for changing an irrational denominator into a rational one. We simply multiply the radical by itself. But then we must multiply the numerator by the same number.
| Example 7. Rationalize this denominator: | 1 |
Solution. Multiply both the numerator and denominator by ![]() :
:
![]()
The denominator is now rational.
2 |
can also take the form ½ |
2 |
= ½ |
For we can write any fraction ![]() as the numerator sime the reciprocal of the denominator.
as the numerator sime the reciprocal of the denominator.
Finally, rationalizing the denominator simplifies the task of evaluating the fraction. Since we know that ![]() , for example, is approximately 1.414, then we can easily know that
, for example, is approximately 1.414, then we can easily know that
| = ½ |
| Problem 11. Rationalize the denominator: | 2 |
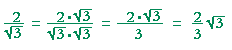
Problem 12. Show each of the following by transforming the left-hand side.
| a) | 6 |
= | 2 |
6 |
= | 3 |
= | 2 |
| b) | 9 |
= | 2 |
9 |
= | 6 |
= | 2 |
| c) | = | ab |
= | b |
Real numbers
![]()
A real number is what we call any rational or irrational number. It is a number we expect to find on the number line. The real numbers are the subject of calculus and of scientific measurement.
A real variable is a variable that takes on real values.
The term real number was coined by René Descartes in 1637. It was to distinguish it from an imaginary or complex number
Problem 13. Let x be a real variable, and let 3 < x < 4. Name five values that x might have.
For example, 3.1, 3.14, ![]() ,
, ![]() ,
, ![]() .
.
Problem 14. If the square root is to be a real number, then the radicand may not be negative. (There is no such real number, for example, as ![]() .)
.)
If ![]() is to be real, then we must have x ≥ 0.
is to be real, then we must have x ≥ 0.
Therefore, what values are permitted to the real variable x ?
a) ![]() x − 3 ≥ 0; that is, x ≥ 3.
x − 3 ≥ 0; that is, x ≥ 3.
b) ![]() 1 + x ≥ 0; x ≥ −1.
1 + x ≥ 0; x ≥ −1.
c) ![]() 1 − x ≥ 0; −x ≥ −1, which implies: x ≤ 1.
1 − x ≥ 0; −x ≥ −1, which implies: x ≤ 1.
d) ![]() x² ≥ 0. In this case, x may be any real number.
x² ≥ 0. In this case, x may be any real number.
Next Lesson: Simplifying radicals
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com