Lesson 11 Section 3
Three Properties of Division
Dividend ÷ Divisor = Quotient
| Dividend Divisor |
= | Quotient |
(The division bar.)
| 1. | A number does not change if we multiply it and then divide the product by the same number: |
| (45 × 100) ÷ 100 = 45; | |
| or if we divide and then multiply the quotient by the same number. | |
| (4500 ÷ 100) × 100 = 4500. | |
We will explain below why that is true .
Because of this property we say that multiplication and division are inverse operations.
| 2. | The quotient will not change if we multiply both the dividend and divisor by the same number; or if we divide them by the same number. |
| 8 2 |
= | 4. | ||
| 3 × 8 3 × 2 |
= | 24 6 |
= | 4. |
| 5 × 8 5 × 2 |
= | 40 10 |
= | 4. |
On dividing the dividend and divisor by the same number:
| 36,000 12,000 |
= | 36,000 ÷ 1000 12,000 ÷ 1000 |
= | 36 12 |
= | 3. |
| 360 120 |
= | 360 ÷ 10 120 ÷ 10 |
= | 36 12 |
= | 3. |
We see, then, that when the dividend and divisor end in the same number of 0's, we may ignore them, and divide the numbers that remain.
| Example 1. | 1200 ÷ 30 = 120 ÷ 3 = 40. |
| Check: 40 × 30 = 1200. | |
| Example 2. | 1.2 30 |
= ? |
Answer. To simplify things, we can make the dividend a whole number by multiplying it by 10. But then we must multiply the divisor also by 10:
| 1.2 30 |
= | 12 300 |
Next, divide by 3. And finally, divide by 100. (Lesson 4.)
| 12 300 |
= | 4 100 |
= .04 |
We will now see how to apply Property 2 when the divisor is a decimal. Because the divisor may not be a decimal. The divisor must be a whole number![]()
Example 3. The divisor a decimal. How many times is .2 contained
in 6?
| Answer. .2 is the divisor: | 6 .2 |
. But in order to divide, |
The divisor must be a whole number.
Therefore we must make .2 into a whole number. To do that, multiply it by 10. But then we must multiply 6 by 10 also:
| 6 .2 |
= | 10 × 6 10 × .2 |
= | 60 2 |
= 30. |
This example illustrates that, even though we say we are dividing decimals, we can really divide only whole numbers, and then correctly place the decimal point. We will see that again in Lesson 13.
| Example 4. | 1.8 .03 |
= | 1.8 × 100 .03 × 100 |
= | 180 3 |
= 60. |
Why did we multiply by 100? Because that makes the divisor .03 into the whole number 3.
In other words:
If the divisor is a decimal, make it a whole number
by multiplying it by 10, or 100, or 1000, etc., according
to the number of decimal digits. Then multiply the dividend
by that same power of 10.
In Lesson 12, we will see how to proceed when the dividend is a decimal.
| 3. | When division is signified by the division bar, and the dividend is composed of factors, then we may divide any one of the factors. |
| 1) | 12 × 8 2 |
= 6 × 8 = 48, |
on dividing 12 by 2.
Or,
| 2) | 12 × 8 2 |
= 12 × 4 = 48, |
on dividing 8 by 2.
Or, finally, on multiplying first:
| 3) | 12 × 8 2 |
= | 96 2 |
= 48. |
These three possibilities imply:
When division is signified by the division bar, then the order
in which we multiply or divide does not matter. We may either divide first or multiply first.
It is more skillful however to divide first because we then have smaller numbers to multiply.
*
Also, if we decompose the dividend into factors, then we can sometimes find a multiple of the divisor.
| 72 4 |
= | 8 × 9 4 |
= 2 × 9 = 18. |
| 700 25 |
= | 100 × 7 25 |
= 4 × 7 = 28. |
For the explanation why Property 3 is true, see below.
Explanation of the properties of division
Arithmetic is the first science. We look at facts themselves. We will explain the properties of division by looking at the arithmetical meanings of multiplication and division, and the relationship between them. This is not algebra.
| 1. | A number does not change if we multiply it and then divide the product by that same number; or if we divide it and then multiply the quotient by that same number. |
To illustrate that, let us start with 5, and then multiply it by 3:
![]()
3 × 5
And now, let us divide by 3. Let us repeatedly subtract 3's. But since 15 is now composed of 5's, how can we do that?
According to the order property of multiplication,
3 × 5 = 5 × 3.
![]()
And so the product is made up of 3's -- it is made up of five 3's.
15 ÷ 3 = 5.
Hence we are back where we started, at 5.
The student should realize that the multiplication table -- 3 × 5 = 15 -- is not the point here. The point is to understand -- to see -- that while 3 × 5 is a sum of 5's, we can still subtract 3's.
This property holds for any numbers.
(206 × 19) ÷ 19 = 206.
Understanding that has nothing to do with knowing the "answer" to 206 × 19![]()
Next, let us start with 15 and divide it by 5:
![]()
We will get 3 because
3 × 5 = 15.
But according to the order property,
5 × 3 = 15.
![]()
Therefore, if we now multiply 3 by 5, we will get back to 15.
| 2. | The quotient will not change if we multiply both the dividend and divisor by the same number; or if we divide them by the same number. |
The quotient is the number of times the divisor is contained in the dividend.
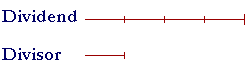
As many times, then, as we increase or decrease the dividend -- and do not change the divisor -- the quotient will increase or decrease that same number of times.

If we double the dividend, the divisor will go in twice as many times, that is, the quotient will double. If we triple the dividend, the quotient will triple.
On the other hand, if we divide the dividend by 2, that is, is we take half of it --

-- then the quotient will also be half. And so on.
Next, as many times as we increase or decrease the divisor -- and do not change the dividend -- then, inversely, the quotient will decrease or increase that same number of times.
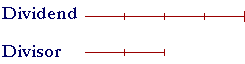
If we double the divisor, the quotient will be half. If we triple the divisor, the quotient will be one third as much.
On the other hand, if we take half of the divisor --
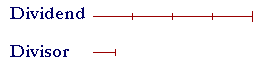
-- it will go in twice as many times. If we divide the divisor by 3, the quotient will triple. And so on.
Therefore, if we increase or decrease the dividend and the divisor the same number of times, the quotient will not change.
In other words: The quotient will not change if we multiply the dividend and divisor by the same number, or if we divide them by the same number.
| 3. | When the dividend is composed of factors, we may divide any one of the factors. |
(3 × 20) ÷ 5 = 3 × (20 ÷ 5)
That is, to divide 3 × 20 by 5, we may first divide 5 into 20, and then multiply by 3.
Here is (3 × 20) ÷ 5 -- Three 20's divided by 5:
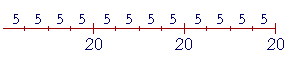
But that is the same as (20 ÷ 5) --
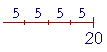
-- added three times. Therefore,
(3 × 20) ÷ 5 = 3 × (20 ÷ 5).
Please "turn" the page and do some Problems.
or
Continue on to the next Lesson.
Section 1 of this Lesson: The meaning of division
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
