Lesson 9
THE MEANING OF MULTIPLICATION
Mental Calculation
In this Lesson, we will answer the following:
- What is the problem of "multiplication"?
- How do we multiply whole numbers that end in 0's?
- How do we multiply mentally by decomposing the multiplier?
How to square a number mentally.
- What is the distributive property of multiplication?
- How can we apply the distributive property to mental calculation?
- How can we multiply mentally by rounding off?
| 1. | What is the problem of "multiplication"? |
| 3 × 5 | |
|
We are to name the number that results from repeatedly adding one number, called the multiplicand, as many times as there are ones in another number, called the multiplier. That number we name is called the product of the two numbers. |
|
3 × 5
We read that "3 times 5 ." × is the multiplication sign. It means:
5 three times.
| 3 × 5 | = | 5 + 5 + 5 |
| = | 15. | |
5 is the multiplicand. We have multiplied it—repeatedly added it—as many times as there are ones in 3 --
3 = 1 + 1 + 1
-- which is the multiplier. (In the United States we write the multiplier on the left: 3 × 5.) The product is 15.
We say that 3, the multiplier, multiplies 5.
Multiplication, then, is an abbreviation for repeated addition.
(We will come to the most general definition of multiplication in Lesson 27.)
The numbers produced—the products—that result from repeatedly adding a number are called its multiples. Here, for example, are the first few multiples of 6:
6, 12, 18, 24, 30, 36.
In practice, of course, to name the product of 5 × 6, the student should not actually add 6 five times: 6 + 6 + 6 + 6 + 6—that would not be skillful. Skill in multiplication depends on knowing the multiplication table, which is a table of repeated additions. Not only is skill in written calculation based on knowing that table, it is the basis of mental calculation. In this Lesson we continue to emphasize problems that do not require a calculator; problems that an educated person should not have to write down.
For many problems, mental calculation has always been the quickest and the most practical.
Example 1. A case of fruit juice contains 9 bottles. How many bottles are there in 4 cases?
| Answer. 4 × 9 bottles | = | 9 + 9 + 9 + 9 |
| = | 36 bottles. |
This illustrates that the product will be the same kind of quantity as the multiplicand; in this case, bottles. The multiplier (4) will be a pure number. It indicates how many times to add the multiplicand.
The student of course should know that 4 × 9 = 36.
The order property of multiplication
If two numbers multiply one another, then the numbers produced
will equal one another.
6 × 4 = 4 × 6.
6, on multiplying 4, will produce the same number
as when 4 multiplies 6.
Now, 6 and 4 are small numbers, and we know that in each case the product is 24.
But consider
9 × 48 and 48 × 9.
If we add 48 nine times, is it obvious that we will get the same number as when we add 9 forty-eight times?
It is not obvious, but we can prove that it is true. And it has nothing to do with knowing the product of 9 × 48.
It will be simpler however to see that
Three 4's = Four 3's.
The principle will be the same.
Consider this array:

If we look at the three columns, we see
Three 4's.
But if we look at the four rows we see
Four 3's.
And they are equal.
3 × 4 = 4 × 3.
And we did not need to know the product.
That is is the order property of multiplication.
In algebra, "multiplication" is not defined, and therefore algebra cannot prove its basic properties. They are stated as laws or axioms. But in arithmetic we define multiplication and therefore we can prove its properties. And it is only because the order property is true in arithmetic, that in algebra what is called the commutative law will apply to arithmetic.
See Appendix 4, Two Theorems.
We now turn our attention to certain skills.
The order of any factors
When numbers are multiplied, they are called the factors of the product.
2 × 3 × 5
The factors are 2, 3, and 5.
The order of any number of factors does not matter.
2 × 3 × 5 = 5 × 2 × 3 = 5 × 3 × 2
And so on. If we were to do the multiplications from left to right, then in each case we will get 30. Therefore we may group factors as we please.
Example 2. Multiply as easily as you can: 7 × 2 × 9 × 5
Solution. Take advantage of factors that produce a multiple of 10:
7 × 2 × 9 × 5 = (2 × 5) × (7 × 9) = 10 × 63 = 630.
(Lesson 4.)
Here is another essential skill:
| 2. | How do we multiply whole numbers that end in 0's? |
| 200 × 30 | |
| Ignore those final 0's and multiply the numbers that remain. Then, put back all the 0's that you ignored. | |
Example 3. 200 × 30 = 6000.
Ignore the final 0's and simply multiply
2 × 3 = 6.
Now we ignored a total of three 0's. Therefore we must put back those three 0's:
200 × 30 = 6000.
When we ignore the 0's, we are just waiting to multiply by the power of 10 that has those 0's.
| 200 × 30 | = | 2 × 100 × 3 × 10 |
| = | 2 × 3 × 100 × 10 | |
| = | 6 × 1000 | |
| = | 6000. | |
Or, when we ignore final 0's, we could say that we have divided by a power of 10. (Lesson 2, Question 10.)
Therefore to compensate and name the right answer, we must multiply by that power—we must add on the same number of 0's. For a number does not change if we divide it and then multiply by the same number. (Lesson 11.)
Example 4. 9 × 20 = 180.
Example 5. Multiply 3 × $.40 mentally.
Answer. Ignore the decimal point for the moment, and we have
3 × 40 = 120.
Now put back those two decimal digits:
3 × $.40 = $1.20
(We will explain in the next Lesson about ignoring decimal points and then replacing them. After all, we can only do arithmetic with whole numbers, anyway![]() )
)
Example 6. 7 × $.80 = $5.60
Decomposing the multiplier
Since multiplication is repeated addition, we can often go from what we know to what we do not know. Say, for example, that you do not know 12 × 8. But Twelve 8's are made up of

Ten 8's are 80,
Two 8's are 16.
Therefore,
Twelve 8's are 80 + 16 = 96.
In this way, we "repeatedly added" Twelve 8's. We decomposed them—broke them up—into
Ten + Two.
| 3. | How do we multiply mentally by decomposing the multiplier? | |||||||||||||||
|
||||||||||||||||
| Decompose the multiplier mentally into its units, typically into its tens and ones. Multiply by the number of tens, then by the number of ones, and add those partial products. | ||||||||||||||||
Since it is true in arithmetic that we may multiply by decomposing the multiplier, the right-hand distributive law of algebra may be applied to arithmetic.
Example 7. Multiply 16 × 5 mentally by decomposing 16 into its tens and ones.
| Answer. Sixteen 5's are equal to | Ten 5's + Six 5's: |
| 50 + 30 = 80. | |
Example 8. Calculate 34 × 6 mentally by decomposing 34.
Solution. 34 × 6 = 30 × 6 + 4 × 6 = 180 + 24 = 204.
"Thirty-four 6's are equal to Thirty 6's plus four 6's."
Example 9. Multiplying by 11. 11 × 45.
Multiplication by 11 is particularly easy because 11 is 10 + 1.
11 × 45 therefore is 10 × 45 + 1 × 45:
450 + 45 = 495.
In other words, to multiply by 11, simply add 10 times the number to the number.
Example 10. 11 × 6.2 = 62 + 6.2 = 68.2
To do this, or any of these, problems in writing --
![]()
-- is nothing more than a written trick to get the right answer.
Example 11. How much is 13 × 12?
Answer. If you know that
12 × 12 = 144,
then 13 × 12 is simply one more 12:
13 × 12 = 144 + 12 = 156.
Or, we could count the 12's like this:
| Thirteen 12's | = Ten 12's + Three 12's | |
| = 120 + 36 | ||
| = 156. | ||
How to square a number mentally
A square figure is a four-sided figure in which all the sides are equal

and all the angles are right angles.
To "square" a number means to multiply it by itself.
"9 squared" = 9 × 9 = 81.
To find the area of a square figure—that is, the space enclosed by the four straight lines—square the length of a side. (See Lesson 10.) If each side were measured by number 6, for example, then the area would be measured by 6 × 6 = 36.
Now, say that we want to square a two-digit number such as 24, mentally. The following geometrical arithmetic illustrates how.
Look at this square figure in which each side is 24.
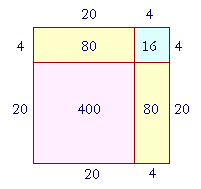
Then the area of that square will be 24 × 24. But we can break up 24 into 20 + 4. Therefore the entire square will be composed of the following:
The square of 20, which is 400.
Two rectangles, each with area 20 × 4 = 80.
And the square of 4, which is 16.
In other words, the square of 20 + 4 is equal to
The square of 20, plus
Two times 20 × 4, plus
The square of 4.
400 + 160 + 16 = 576.
That is not a difficult mental calculation.
Example 12. Square 52.
Solution. 52 = 50 + 2.
The square of 50 + 2 is equal to
The square of 50, plus
Two times 50 × 2, plus
The square of 2.
2500 + 200 + 4 = 2704.
Problem 1. Square 35.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
The square of 30 + 5 is equal to:
The square of 30 + Two times 30 × 5 + The square of 5.
900 + 300 + 25 = 1225.
Example 13. Square 48.
Solution. Rather than square 40 + 8, it is simpler to square 50 − 2.
The square of 50 − 2 equals
The square of 50, minus
Two times 50 × 2, plus
The square of 2.
2500 − 200 + 4 = 2304.
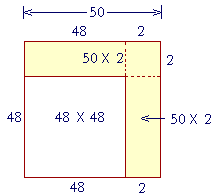
The entire square is the square of 50. It is composed of the square of 48, plus two rectangles, 50 × 2—which we must subtract. But we should not subtract the square of 2 twice. Therefore we add it at the end.
Problem 2. Square 39.
The square of 40 − 1 is equal to:
The square of 40 − Two times 40 × 1 + The square of 1.
1600 − 80 + 1 = 1521.
At this point, please "turn" the page and do some Problems.
or
Continue on to the Section 2:
The distributive property of multiplication
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
