Lesson 16
PARTS
OF NATURAL NUMBERS 2
This Lesson depends on Parts of Natural Numbers 1
In this Lesson, we will answer the following:
- How can we take a part of a number that ends in 0's?
- How can we find a part of a number by decomposing it?
- How can we divide by taking a part?
- What do we mean by a mixed number of times?
- How do we increase or decrease a number by a given part?
- What percent means a third?
- Which natural numbers are called the even numbers?
- What number is half of 1?
- How can we take half of an odd number?
- How can we take a fourth or 25% of a number?
- How can we multiply by 5?
- How can we take 5% of a number?
- How can we multiply by 15?
- How can we take 15% of a number?
| 1. | How can we take a part of a number that ends in 0's? |
| A third of 120 | |
| Ignore the 0's and take that part of what remains; then, put back the 0's. | |
Example 1. How much is a third of 120?
Answer. Ignore the 0. Then
A third of 12 is 4.
A third of 120 is 40.
Similarly,
A third of 1,200 is 400.
A third of 120,000 is 40,000.
It is a 4 followed by four 0's.
Example 2. How much is a third of $1.20?
Solution. Ignore the decimal point. A third of 120 is 40. Now replace the decimal point. A third of $1.20 is $.40.
Ignoring decimal points is typical in practically all problems involving decimals. (Compare Lesson 9.)
Example 3. How much is a fifth of $4.50?
Solution. Ignore the decimal point. A fifth of 450 is 90. (A fifth of 45 is 9.) Therefore a fifth of $4.50 is $.90.
Example 4. How much is an eighth of 4,000?
Answer. If we ignore all the 0's, then we cannot take an eighth of 4. But if we ignore only two 0's, then
An eighth of 40 is 5.
Therefore,
An eighth of 4000 is 500.
Decomposing
Example 5. How much is half of 112?
Solution. Just as we can divide by decomposing, so we can find a part of a number. We can easily decompose 112 into two numbers whose half we know:
112 = 100 + 12.
Half of 100 is 50. Half of 12 is 6. Therefore, half of 112 is 56.
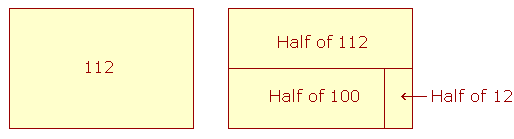
We see then that to find a part of a sum -- of 100 + 12 -- we may find that part of each term of the sum, and then add.
Half of 112 = Half of 100 + Half of 12.
This is also true for adding parts, plural:
| Three fourths of 108 | = | Three fourths of 100 + Three fourths of 8 |
| = | 75 + 6 | |
| = | 81. | |
See the theorems below.
To summarize:
| 2. | How can we find a part of a number by decomposing it? |
| Decompose it into two or more numbers that clearly have that part. Take that part of each, and add. | |
Example 6. How much is a third of 252?
Solution. Upon decomposing 252 into 240 + 12:
| A third of 252 | = | A third of 240 + A third of 12 |
| = | 80 + 4 | |
| = | 84. | |
Why did we choose 240? Because, since 24 has an exact third, then so does 240. And 240 is close to 252.
Example 7. Three people go to lunch and the bill is $32.40. How much does each one pay?
Solution. We must find a third of $32.40. Now, a third of $30 is $10. A third of the remainder, $2.40, is $.80. (Compare Example 2.) Each one will pay $10.80.
Example 8. How much is a fifth of $47.50
Solution. What number closest to 47 has an exact fifth? 45. Therefore decompose $47.50 into
$45 + $2.50.
A fifth of $45 is $9.
A fifth of $2.50 is $.50.
Therefore, a fifth of $47.50 is $9.50.
According to Lesson 15, we have found that $9.50 is 20% of $47.50.
Also in Lesson 15, we saw that to calculate a part of a number, divide. Symmetrically, then, to divide we may take a part.
| 3. | How can we divide by taking a part? |
| 500 ÷ 2 | |
| Take the part that corresponds to the name of the divisor. To divide by 2, take half. To divide by 3, take a third. And so on. |
|
Example 9. There are 500 envelopes in a box. If you use 2 envelopes every day, how many days until the box will be empty?
Solution. How many 2's are there in 500? This is a division problem. The divisor is 2. Therefore take half. Half of 500 is 250. The box will be empty in 250 days.
Now, to divide by 2 does not mean to take half. (It means to name the number of 2's.) But by taking half we can know how many 2's.
For,
2 × 250 = 500.
That means that 250 is half of 500.
But that implies
250 × 2 = 500.
That means there are two hundred fifty 2's in 500. And we could know that by taking half.
Compare Lesson 11, Example 6.
Example 10. How many 3's are there in 252?.
Solution. This is a division problem: 252 ÷ 3. To answer, take a third of 252. That was Example 6. 252 ÷ 3 = 84.
| 4. | What do we mean by a mixed number of times? |
| A whole number of times plus a part. | |
Example 11. How much is two and a half times 8?
Answer. "Two and a half times 8" means
Two times 8 plus half of 8.
Two times 8 is 16. Half of 8 is 4. 16 plus 4 is 20.
Example 12. A cheese sells for $6 a pound, and you buy three and a half pounds. How much do you pay?
| Answer. | Three pounds cost $18. |
| Half a pound costs $3. | |
| You pay $21. | |
That is, "Three and a half times 6" means
Three times 6 plus half of 6.
18 + 3 = 21.
That is a mixed number of times: A whole number of times plus a part.
Example 13. How much is five and a quarter times 8?
| Answer. | "Five times 8 is 40. |
| "A quarter (or a fourth) of 8 is 2. | |
| "40 + 2 = 42." | |
| 5. | How do we increase or decrease a number by a given part? |
| To increase by a given part, add that given part; to decrease, subtract. |
|
Example 14. A jacket originally sold for $150.
a) It now sells for a third more. What is the present price?
Answer. A third of $150 is $50. It now sells for $50 more. It sells for $200.
b) It now sells for a third less. What is the present price?
Answer. $150 − $50 = $100.
Example 15. A photograph measures 8 inches by 12 inches.
a) Each side will be increased by one quarter. What are the new dimensions?
Answer. A quarter of 8 is 2. A quarter of 12 is 3. The new dimensions are:
(8 + 2) inches by (12 + 3) inches = 10 inches by 15 inches.
b) Each side will be reduced by one quarter. What are the new dimensions?
Answer. (8 − 2) inches by (12 − 3) inches = 6 inches by 9 inches.
| 6. | What percent means a third? | |
| For the explanation why, see the following Example. | ||
Example 16. The percent that means a third.
a) In a recent exam, a third of the class got A. What percent got A?
Answer. Since the whole class is 100%, then a third of the class will be a third of 100%. We must divide 100 by 3. It will not be a whole number. (Lesson 11.)
| 100 3 |
= | 99 + 1 3 |
= 33 + | 1 3 |
= 33 | 1 3 |
. |
| 33 | 1 3 |
% of the class got A. |
| We see, then, that 33 | 1 3 |
% means a third. |
Again, percents are parts of 100%. Just as 50% means half, because 50 is half of 100; and 25% means a quarter because 25 is a quarter of 100; so 33![]() % means a third. 33
% means a third. 33![]() is a third of 100.
is a third of 100.
b) What percent means two thirds?
| Answer. Two thirds of 100 will be 2 × 33 | 1 3 |
: |
| 2 × 33 | 1 3 |
= | 2 × 33 | + 2 × | 1 3 |
. |
| 2 × 33 | = 66 . 2 × | 1 3 |
= | 1 3 |
+ | 1 3 |
= | 2 3 |
. |
| 2 × 33 | 1 3 |
= | 66 | 2 3 |
. |
| 66 | 2 3 |
% means two thirds. |
In Section 2, Question 10, we will see a simple way to find a quarter or 25% of a number.
Percent continues in Lessson 17.
Example 17. Calculator problem. How much is five eighths of $650.16?
Solution. To find five eighths, we must first find one eighth, and then multiply by 5. Press
| 6 | 5 | 0 | . | 1 | 6 | ÷ | 8 | = | × | 5 | = |
See:
| 406.35 |
Two theorems
We have seen that
Half of 100 + Half of 12 = Half of (100 + 12).
Here is the theorem:
| 1. | The sum of the same part of numbers is that same part of the sum of those numbers. |
| Euclid, VII, 5. | |
Let the number A be a part of number C, and let number B be the same part of number D.
Then the sum of A and B will be that same part of the sum of C and D.
For since A is the same part of C that B is of D, there are as many numbers in C equal to A as there are in D equal to B.

Therefore divide C into the numbers equal to A, namely G, H, I,
and divide D into the numbers equal to B, namely J, K, L;
thus C and D have been divided into the same number of parts.
Then since G is equal to A, and J equal to B, the sum of G and J is equal to the sum of A and B.
For the same reason, the sum of H and K, and the sum of I and L, are also equal to the sum of A and B.
Therefore, as many numbers as there are in C equal to A, so many are there in the sum of C and D equal to the sum of A and B.
Therefore, whatever multiple C is of A, the sum of C and D is the same multiple of the sum of A and B.
Therefore, whatever part A is of C, the sum of A and B is the same part of the sum of C and D.
Which is what we wanted to prove.
*
That property of numbers is also true for parts, plural. For example:
Three fifths of 100 + Three fifths of 10 = Three fifths of (100 + 10).
Here is the theorem:
| 2. | The sum of the same parts of numbers is equal to the same parts of the sum of those numbers. |
| Euclid, VII, 6. | |

Let the number A be the same parts of number C that number B is of number D.
Then the sum of A and B will be the same parts of the sum of C and D.
For since A is the same parts of C that B is of D, there are as many numbers in A equal to a part of C as there are in B equal a part of D.

Divide A into those numbers equal to a part of C, namely G, H, I. And divide B into those numbers equal to a part of D, namely J, K, L;
thus A and B have been divided into the same number of parts.
Then since G is the same part of C that J is of D, the sum of G and J is that same part of the sum of C and D. (Theorem 1.)
For the same reason, the sum of H and K, and the sum of I and L, are also that same part of the sum of C and D.
Therefore, whatever parts A is of C, the sum of A and B is the same parts of the sum of C and D.
Which is what we wanted to prove.
Since these are true theorems of arithmetic, then—when when multiplication by a fraction a is defined as in Lesson 27—the factoring axiom of algebra,
ab + ac = a(b + c),
can be applied to arithmetic.
At this point, please "turn" the page and do some Problems.
or
Continue on to the Section 2.
1st Lesson on Parts of Natural Numbers
Introduction | Home | Table of Contents
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
