Book I. Propositions 29 and 30
Problems
Back to Proposition 29.
11. State Postulate 5.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
If a straight line that meets two straight lines makes the interior angles on the same side less than two right angles, then those two straight lines, if extended, will meet on that same side.
12. a) State the hypothesis of Proposition 29.
Two straight lines are parallel.
2. b) State the partial conclusion.
A straight line that meets them makes the alternate angles equal.
2. c) Practice Proposition 29 up to that conclusion.
13. Name four ways of knowing that two angles are equal.
They are corresponding angles of congruent triangles.
They are vertical angles.
When a straight line meets two parallel lines, they are the alternate angles.
They are right angles.
14. Complete the proof of Proposition 29; use the conclusion that the
14. alternate angles are equal.
14. a) If two straight lines are parallel, then a straight line that meets them makes
14. a) an exterior angle equal to the opposite interior angle on the same side.
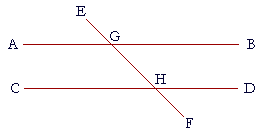
Apply the enunciation to the figure, and prove it.
Let the straight lines AB, CD be parallel, and let the straight line EF meet them;
then the exterior angle EGB is equal to the opposite interior angle on the same side, GHD.
For, since the straight lines AB, CD are parallel,
the alternate angles AGH, GHD are equal. (I. 29)
But angle EGB is equal to angle AGH,
because they are vertical angles.
Therefore angle EGB is equal to angle GHD. (Axiom 1)
3. b) If two straight lines are parallel, then a straight line that meets them makes
3. b) the interior angles on the same side equal to two right angles.

Apply the enunciation to the figure, and prove it. The proof follows
3. b immediately from part a).
3. (Hint: How could two angles possibly be equal to two right angles?)
Let the straight lines AB, CD be parallel, and let the straight line EF meet
them;
then the interior angles on the same side, namely angles BGH, GHD, are together equal to two right angles.
For, to each of the equal angles EGB, GHD (Part a)
join angle BGH.
But angles EGB, BGH are together equal to two right angles. (I. 13)
Therefore angles BGH, GHD together are also equal to two right angles. (Axiom 1)
Q.E.D.
15. Here is Playfair's Axiom:
Two intersecting straight lines cannot both be parallel to a third line.
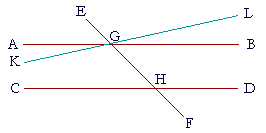
5. Apply that enunciation to the figure, and use Problem 4b to
5. prove it.
Let the straight lines AB, CD be parallel,
and let the straight line EF meet them at the points G, H respectively;
then AB is the only straight line parallel to CD that passes through the point G.
For, suppose that the straight line KL that passes through G is also parallel to CD.
Then the interior angles on the same side, angles KGH, GHC
are together equal to two right angles. (Problem 4b)
But the interior angles AGH, GHC
are also equal to two right angles, because AB is also parallel to CD.
From those pairs of equals, take away angle GHC.
Therefore, angle KGH is equal to angle AGH, the smaller to the larger,
which is absurd.
Therefore two intersecting straight lines cannot both be parallel to a third line.
16. If a straight line is perpendicular to one of two parallel lines, then it
is
16. also perpendicular to the other line.
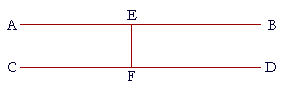
Apply that enunciation to the figure, and prove it.
Let the straight lines AB, CD be parallel,
and let EF be perpendicular to AB;
then EF is also perpendicular to CD.
For, angle AEF is equal to angle EFD
because they are alternate angles.
But angle AEF is equal to angle BEF
because, by hypothesis, they are right angles.
Therefore angle BEF is equal to angle EFD. (Axiom 1)
But angle BEF is equal to angle EFC
because they are alternate angles;
therefore angle EFC is equal to angle EFD. (Axiom 1)
Therefore EF is perpendicular to CD. (Definition 3)
17. Proposition 30.
Straight lines that are parallel to the same straight line are parallel
to each other.
Apply the enunciation to a figure, and prove it.
Prove the following:
18. When a straight line meets two parallel straight lines, then the bisectors of the
17. interior angles on the same side are perpendicular to one another.
19. If the straight line that bisects the exterior angle of a triangle is parallel to the
19. base, then the triangle is isosceles.
10. Triangle ABC is isosceles with AB equal to AC. Find the points
10. D, E on them respectively such that BD, DE, EC are all equal.
Table of Contents | Introduction | Home
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com