Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

VERTICAL ANGLES
Book I. Proposition 15
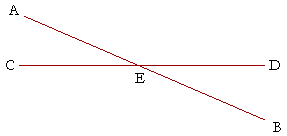
WHEN TWO STRAIGHT LINES AB, CD intersect one another, then angles AEC, DEB are called vertical angles (or vertically opposite), as are angles AED, CEB. Those are the two pairs of vertical angles that intersecting straight lines form.
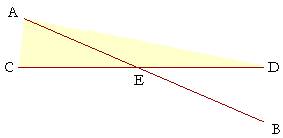
Now, angles AEC, AED together are equal to two right angles (Proposition 13),
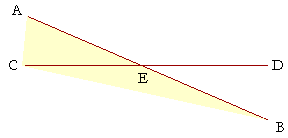
as are angles AEC, CEB. Therefore if we take away angle AEC from each pair --
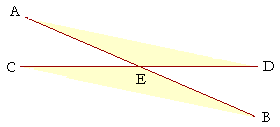
-- then we can see that angle AED will equal angle CEB. The vertical angles are equal.
That is the next theorem.
PROPOSITION 15. THEOREM
| When two straight lines intersect one another, the vertical angles are equal. | |
| Let the straight lines AB, CD intersect one another at the point E; | |
| then angle AED is equal to angle CEB, | |
| and angle AEC is equal to angle DEB. | |
 |
|
| For, since the straight line AE stands on the straight line CD, | |
| making angles AEC, AED, | |
| then those angles are equal to two right angles. | (I. 13) |
| And since the straight line CE stands on the straight line AB, | |
| making angles AEC, CEB, | |
| then those angles also are equal to two right angles. | |
| Therefore, | |
| angles AEC, AED are equal to angles AEC, CEB. | |
| (Postulate 4 and Axiom 1) | |
| From each pair, take angle AEC. | |
| Therefore the remaining angle AED is equal to the remaining angle CEB. | (Axiom 3) |
| Similarly, we can prove that angles AEC, DEB are equal. | |
| Therefore, when two straight lines etc. Q.E.D. | |
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com