Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

RELATIONS AMONG THE
ANGLES OF A TRIANGLE
Book I. Propositions 16 and 17
THE FOLLOWING PROPOSITION is basic to the theory of parallel lines. It also provides an excellent example of how constructions are used creatively to prove a point.
PROPOSITION 16. THEOREM
| If one side of a triangle is extended, then the exterior angle is greater than either of the opposite interior angles. | |
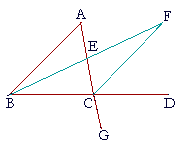
| Let ABC be a triangle, and let one side of it BC be extended to D; then the exterior angle ACD is greater than either of the opposite interior angles, ABC, CAB. |
|
 |
|
| (We now draw triangle BFC in such a way that triangles BAE, ECF will be congruent; that makes angle BAE equal to angle ECF. Eventually, Proposition 27, that will imply that the lines BA, CF are parallel.) | |
| Bisect AC at E; | (I. 10) |
| draw BE and extend it in a straight line to F, making EF equal to BE; |
(I. 3) |
| draw FC, and extend AC to a point G. | |
| Then, since AE is equal to EC, and BE to EF, | |
| the two sides AE, EB are equal to the two sides CE, EF respectively; | |
| and angle AEB is equal to angle CEF, | |
| because they are vertical angles. | (I. 15) |
| Therefore triangles AEB, CEF are congruent, | (S.A.S.) |
| and the remaining angles are equal to the remaining angles, namely those that are opposite the equal sides: | |
| angle BAE is equal to angle ECF. | |
 |
|
| But angle ECD is greater than angle ECF; | (Axiom 5) |
| therefore angle ACD is greater than angle BAE. | |
| If we bisect BC, in the same way then we can prove that angle BCG, | |
| that is, angle ACD, | (I. 15) |
| is greater than angle ABC as well. | |
| Therefore, if one side of a triangle etc. Q.E.D. | |
PROPOSITION 17. THEOREM
| Any two angles of a triangle are together less than two right angles. | |
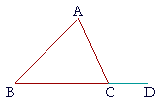
| Let ABC be a triangle; then any two of its angles are together less than two right angles. |
|
 |
|
| Extend BC to D. | |
| Then, since ACD is the exterior angle of the triangle,
it is greater than opposite interior angle ABC. |
(I. 16) |
| To each of those join angle ACB. | |
| Then | |
| angles ACD, ACB are greater than angles ABC, ACB. | |
| But angles ACD, ACB are together equal to two right angles. | (I. 13) |
| That is, | |
| two right angles are greater than angles ABC, ACB. | |
| Therefore angles ABC, ACB are together less than two right angles. | |
| In the same way we could show that angles BAC, ACB, and also angles CAB, ABC, are together less than two right angles. | |
| Therefore, any two angles etc. Q.E.D. | |
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com