Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

EQUALITY OF NON-CONGRUENT FIGURES
Book I. Propositions 35 and 36
WE SPEAK OF PARALLELOGRAMS that are "in the same parallels."
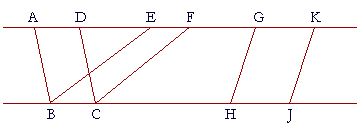
Thus if AK, BJ are parallel, then the parallelograms ABCD, GHJK are in the same parallels.
Further, two parallelograms may be "on the same base and in the same parallels," as are ABCD and EBCF. They are on the same base BC, and in the same parallels AF, BC.
Equality of non-congruent figures
If the theorem about the three angles of a triangle was the first triumph of the theory of parallel lines (I. 32), then the following theorem is the second, because it establishes how we can know when figures that are not congruent are equal.
The theorem proves that parallelograms on the same base and in the same parallels are equal.
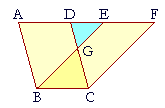
Parallelograms ABCD, EBCF are on the same base BC and in the same parallels AF, BC. We can then show that triangles ABE, DCF are equal (S.A.S). On subtracting DGE from those triangles and then adding GBC, we can see that the resulting parallelograms are equal!
PROPOSITION 35. THEOREM
| Parallelograms on the same base and in the same parallels are equal. | |
| Let ABCD, EBCF be parallelograms on the same base BC and in the
same parallels AF, BC; then ABCD and EBCF are equal areas. |
|
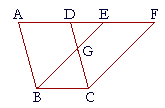 |
|
| For, since ABCD is a parallelogram, | |
| AD is equal to BC. | (I. 34) |
| For the same reason, | |
| EF is equal to BC, so that AD is equal to EF. |
(Axiom 1) |
| Therefore if we join DE to each, | |
| the whole AE is equal to the whole DF. | (Axiom 2) |
| Now, AB is equal to DC; | (I. 34) |
| therefore the two sides EA, AB of triangle EAB | |
| are equal respectively to the two sides FD, DC of triangle FDC; | |
| and the exterior angle FDC is equal to the interior angle EAB; | (I. 29) |
| therefore triangle EAB is equal to triangle FDC. | (S.A.S.) |
 |
|
| Take triangle DGE from each one; | |
| then the quadrilateral ABGD which remains is equal to the quadrilateral FEGC which remains. | (Axiom 3) |
| Join triangle GBC to each quadrilateral; | |
| then the whole parallelogram ABCD is equal to the whole parallelogram EBCF. | (Axiom 2) |
| Therefore, parallelograms on the same base etc. Q.E.D. | |
![]()
PROPOSITION 36. THEOREM
| Parallelograms on equal bases and in the same parallels are equal. | |
| Let ABCD, EFGH be parallelograms on equal bases BC, FG, and in the same parallels AH, BG; then ABCD is equal to EFGH. |
|
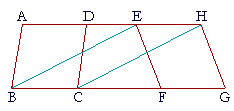 |
|
| Draw BE, CH. | |
| Then, since BC is equal to FG, | (Hypothesis) |
| and FG equal to EH, | (I. 34) |
| BC is equal to EH; | (Axiom 1) |
| and they are parallel, | |
| and the straight lines BE, CH join their extremities on the same side. | |
| But straight lines which join the extremities on the same side of two equal and parallel straight lines, are themselves equal and parallel. | (I. 33) |
| Therefore BE, CH are equal and parallel. | |
| Therefore EBCH is a parallelogram. | (Definition 15) |
| And it is equal to ABCD, because they are on the same base BC, and in the same parallels BC, AH. |
(I. 35) |
 |
|
| For the same reason, EBCH is equal to EFGH, | |
| because they are on the same base EH. | |
| Therefore the parallelogram ABCD is equal to the parallelogram EFGH. | (Axiom 1) |
| Therefore, parallelograms on equal bases etc. Q.E.D. | |
![]()
The elementary parallelogram is a rectangle. Figure EFGH.
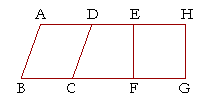
The arithmetical formula for the area of a rectangle is the measure of the base times the measure of the height, where the height is the distance between the parallels.
A = b × h.
From Proposition 36 we may conclude that the area of a parallelogram (ABCD) with equal base and height is also A = b × h.
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com