CONSTRUCTION OF A SQUARE

Book I. Proposition 46

WE ARE JUST ABOUT READY to prove the Pythagorean theorem, which is about the squares that are drawn on the sides of a right-angled triangle. The following proposition will show that the figure we construct satisfies the definition of a square, and therefore that the figure we have called a "square" actually exists. (See the Commentary on the Definitions.)

PROPOSITION 46. PROBLEM

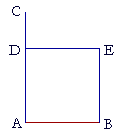
On a given straight line to draw a square.

Let AB be the given straight line; we are required to draw a square on AB.



From the point A draw AC at right angles to the straight line AB,	(I. 11)

and make AD equal to AB;	(I. 3)

through the point D draw DE parallel to AB;	(I. 31)

and through the point B draw BE parallel to AD.

Then ADEB is a square.

For, ADEB is by construction a parallelogram;	(Definition 15)

therefore AB is equal to DE, and AD is equal to BE.	(I. 34)

But AB is equal to AD.

(Construction)

Therefore the four straight lines AD, DE, EB, BA are equal to one another, so that the parallelogram ADEB is equilateral.	(Axiom 1)

Next, all its angles are right angles.

For, since the straight line AD meets the parallel lines DE, AB,
it makes angles BAD, ADE equal to two right angles.

(I. 29)

But angle BAD is a right angle;	(Construction)

therefore angle ADE is also a right angle.

And in a parallelogram the opposite angles are equal;	(I. 34)

therefore each of the opposite angles DEB, EBA is also a right angle.

Therefore ADEB has all its angles right angles.

And we proved that all the sides were equal.

Therefore ADEB is a square,	(Definition 7)
and we have drawn it on the given straight line AB. Q.E.F.

Please "turn" the page and do some Problems.

Continue on to the next proposition.

Previous proposition

Table of Contents | Introduction | Home

Please make a donation to keep TheMathPage online.
Even $1 will help.

Questions or comments?

E-mail: teacher@themathpage.com