Table of Contents | Introduction | Home
![]()
P l a n e G e o m e t r y
An Adventure in Language and Logic
based on

CONGRUENCE 2
Book I. Proposition 8
SUPPOSE THAT two sides of one triangle are equal respectively to
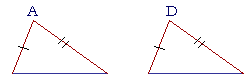
two sides of another. What will be a sufficient condition for the angles that are contained by those sides to be equal, the angles A and D? Because, if those angles are equal, then the triangles will be congruent, Side-angle-side.
A sufficient condition for those angles to be equal . . . is that the bases are also equal.
Again, Euclid proved this by superposition. And again we will accept it as a postulate.
(As for Proposition 7, it was a theorem Euclid needed to prove Proposition 8 by superposition.)
PROPOSITION 8.
If two triangles have two sides equal to two sides respectively, and if the bases are also equal, then those angles will be equal that are contained by the two equal sides.
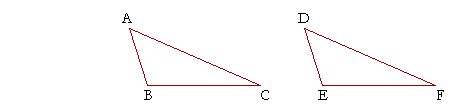
Let triangles ABC, DEF be two triangles, with the two sides AB, AC equal to the two sides DE, DF respectively;
and let the base BC be equal to the base EF;
then angle BAC will equal angle EDF.
![]()
Since those angles are equal, then the triangles are congruent
according to S.A.S. Nevertheless, we will say that this gives a second condition for triangles to be congruent, and we will often refer to this proposition as "S.S.S.": Side-Side-Side.
In the enunciation, it would be redundant to state "the triangles themselves will be equal areas, and the remaining angles will be equal, namely those that are opposite the equal sides," because we have already stated that in S.A.S. See the following Example.
Example. In this figure, AB is equal to DC, and AC is equal to DB. Prove that angle BAC is equal to angle CDB, and that angle ABC is equal to angle DCB.
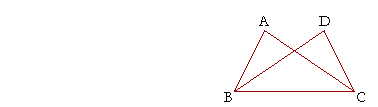
Solution. Since AB is equal to DC, and AC to DB,
then the two sides BA, AC are equal to the two sides CD, DB respectively;
and the base BC is common to triangles BAC, CDB;
therefore, angle BAC is equal to angle CDB (S.S.S.).
Therefore the triangles are congruent,
and those angles are equal that are opposite the equal sides. (S.A.S.)
Therefore angle ABC, opposite side CA, is equal to angle DCB, opposite the equal side BD.
Please "turn" the page and do some Problems.
or
Continue on to the next proposition.
Table of Contents | Introduction | Home
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com