25
THE BINOMIAL THEOREM
Formal statement of the theorem
THE BINOMIAL THEOREM shows how to calculate a power of a binomial—(a + b)n—without actually multiplying.
For example, if we actually multiplied out the 4th power of (a + b) --
(a + b)4 = (a + b)(a + b)(a + b)(a + b)
-- then on collecting like terms we would find:
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 . . . . (1)
Note: The literal factors are all possible terms in a and b where the sum of the exponents is 4: a4, a3b, a2b2, ab3, b4.
The degree of each term is 4.
The first term is actually a4b0, which is a4 · 1.
Thus to "expand" (a + b)5, we would anticipate the following terms, in which the sum of all the exponents is 5:
(a + b)5 = ? a5 + ? a4b + ? a3b2 + ? a2b3 + ? ab4 + ? b5
The question is, What are the coefficients?
They are called the binomial coefficients. In the expansion of
(a + b)4, the binomial coefficients are
1 4 6 4 1
line (1) above.
Note the symmetry: The coefficients from left to right are the same right to left.
The answer to the question, "What are the binomial coefficients?" is called the binomial theorem. It shows how to calculate the coefficients in the expansion of (a + b)n.
The symbol for a binomial coefficient is ![]() . The upper index n is the exponent of the expansion; the lower index k indicates which term, starting with k = 0.
. The upper index n is the exponent of the expansion; the lower index k indicates which term, starting with k = 0.
For example, when n = 5, each term in the expansion of (a + b)5 will look like this:
![]() a5 − kbk
a5 − kbk
k will successively take on the values 0 through 5.
(a + b)5 = ![]() a5 +
a5 + ![]() a4b +
a4b + ![]() a3b2 +
a3b2 + ![]() a2b3 +
a2b3 + ![]() ab4 +
ab4 + ![]() b5
b5
Note: Each lower index is the exponent of b. The first term has k = 0 because in the first term, b appears as b0, which is 1.
Now, what are these binomial coefficients, ![]() ?
?
The theorem states that the binomial coefficients are none other than the combinatorial numbers, nCk .
![]() = nCk
= nCk
| (a + b)5 | = | 5C0a5 + 5C1a4b + 5C2a3b2 + 5C3a2b3 + 5C4ab4 + 5C5b5 |
| = | 1a5 + |
|
| = | a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5 | |
The binomial coefficients here are
1 5 10 10 5 1.
Note the symmetry.
The coefficient of the first term is always 1, and the coefficient of the second term is the same as the exponent of (a + b), which here is 5.
Using sigma notation and factorials for the combinatorial numbers, here is the binomial theorem:
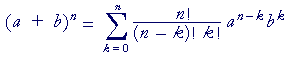
What follows the summation sign is the general term. Each term in the sum will look like that—the first term having k = 0; then k = 1, k = 2, and so on, up to k = n.
Notice that the sum of the exponents (n − k) + k, always equals n.
Example 1.
a) The term a8b4 occurs in the expansion of what binomial?
Answer. (a + b)12. The sum of 8 + 4 is 12.
b) In that expansion, what number is the coefficient of a8b4?
Answer. It is the combinatorial number,
| 12C4 | = | 12· 11· 10· 9 1· 2· 3· 4 |
= 495 |
Note again: The lower index, in this case 4, is the exponent of b.
This same number is also the coefficient of a4b8, since 12C8 = 12C4.
Example 2. Expand (a − b)5.
Solution. We found the binomial coefficients to be 1 5 10 10 5 1. The difference with (a − b) is that the signs of the terms will alternate:
(a − b)5 = a5 − 5a4b + 10a3b2 − 10a2b3 + 5ab4 − b5.
For, a − b = a + (−b), therefore each term will have the form
a5 − k(−b)k.
When k is even, (−b)k will be positive. But when k is odd, (−b)k will be negative.
Each odd power of b will have a minus sign.
Example 3. In the expansion of (x − y)15, calculate the coefficients of x3y12 and x2y13.
Solution. The coefficient of x3y12 is positive because the exponent of
y is even. That coefficient is 15C12. But 15C12 = 15C3, and so we have
| 15· 14· 13 1· 2· 3 |
= | 455. |
The coefficient of x2y13, on the other hand, is negative because the exponent of y is odd. The coefficient is − 15C13 = − 15C2. We have
| − | 15· 14 1· 2 |
= −105. |
Example 4. Write the first four terms of (a + b)n. Do not use factorials.
Solution.
| (a + b)n | = | nC0an + nC1an − 1b + nC2an − 2b2 + nC3an − 3b3 |
| = | an
+ nan − 1b
+ | |
Notice: Each coefficient is a factor of the next coefficient. The coefficient n is a factor of
![]() .
.
That in turn is a factor of
![]() .
.
To construct the next coefficient, then, multiply the present coefficient by the exponent of a in that term—
-- namely n − 3:
| n(n − 1)(n − 2)(n − 3) 1· 2· 3· 4 |
And divide it by 1 more than the exponent of b.
That is the coefficient of an − 4b4.
Example 5. Use the binomial theorem to expand (a + b)8.
Solution. The expansion will begin :
(a + b)8 = a8 + 8a7b
The first coefficient is always 1. The second is always the exponent of the expansion, in this case 8.
The next coefficient can be constructed as described above. It will be the present coefficient, 8 --
(a + b)8 = a8 + 8a7b + 28a6b2
-- times the exponent of a in that term , 7, divided by 1 more then the exponent of b. It will be 8· 7/2 = 28.
The next coefficient --
(a + b)8 = a8 + 8a7b + 28a6b2 + 56a5b3
-- is 28· 6, divided by 3:
28· 6 / 3 = 28· 2 = 56.
The next --
(a + b)8 = a8 + 8a7b + 28a6b2 + 56a5b3 + 70a4b4
-- is 56· 5, divided by 4:
56· 5 / 4 = 14· 5 = 70.
We have now come to the point of symmetry. For, the coefficient of a3b5 is equal to the coefficient of a5b3, which is 56. And so on for the remaining coefficients.
Here is the complete expansion:
| (a + b)8 | = | a8 + 8a7b + 28a6b2 + 56a5b3 + 70a4b4 + 56a3b5 + |
| 28a2b6 + 8ab7 + b8. | ||
Problem 1. In the expansion of (a + b)n, each term has the form
![]() an − kbk,
an − kbk,
where k successively takes on the value 0, 1, 2, . . ., n.
![]() is the symbol for the binomial coefficient.
is the symbol for the binomial coefficient.
The binomial theorem is the statement that ![]() = ?
= ?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
The combinatorial number, nCk.
Problem 2. Use factorials to write the general term in the expansion of (a + b)n.
|
n! (n − k)! k! |
an − kbk |
Problem 3.
a) Calculate the coefficient of a4b6 in the expansion of (a + b)10.
10C6 = 10C4 = 210
b) The coefficient of which other term is the same? a6b4
c) In the expansion of (a + b)n, the coefficient of an − kbk is the same
c) as the coefficient of which other term?
akbn − k
Problem 4. Calculate the coefficient of
a) x17y3 in the expansion of (x + y)20. 1140
b) x3y17 in the expansion of (x + y)20. 1140
c) x3y17 in the expansion of (x − y)20. −1140
d) x2y18 in the expansion of (x − y)20. 190
e) x5y5 in the expansion of (x − y)10. −252
f) x10 in the expansion of (x − 1)15. −3003
Problem 5. Write the first four terms of (x + h)n. Do not use factorials.
| (x + h)n | = | xn + nxn−1h + | n(n − 1) 1· 2 |
xn−2h2 + | n(n − 1)(n − 2) 1· 2· 3 |
xn−3h3. |
Problem 6. Compute the first four terms of each of the following.
a) (a + b)15 a15 + 15a14b + 105a13b2 + 455a12b3
b) (x − 1)20 x20 − 20x19 + 190x18 − 1140x17
Example 6. Write the 5th term in the expansion of (a + b)10.
Solution. In the 1st term, k = 0. In the 2nd term, k = 1. And so on.
The index k—the exponent of b—of each term
is one less than the ordinal number of the term.
Thus in the 5th term, k = 4. The exponent of b is 4. The 5th term is
| 10C4 | a6b4 | = | 10· 9· 8· 7 1· 2· 3· 4 |
a6b4 = 210 a6b4 |
Problem 7. Consider the expansion of (x + b)30.
a) What is the exponent of b in the 25th term? 24
b) In the kth term? k − 1
c) Write the fourth term, with its coefficient. 4,060x27b3
Problem 8. Calculate each of the following.
a) The third term of (a + b)11. 55a9b2
b) The fifth term of (x − y)7. 35x3y4
c) The tenth term of (x − 1)12. −220x3
| d) The fifteenth term of (1 + | 1 x |
)18. 3060x−14 |
| e) The fourth term of (x − | 1 x |
)10. −120x4 |
Pascal's triangle
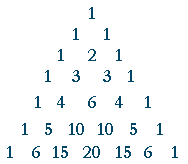
That triangular array is called Pascal's Triangle. Each row gives the combinatorial numbers, which are the binomial coefficients. That is, the row 1 2 1 are the combinatorial numbers 2Ck, which are the coefficients of (a + b)2. The next row—
1 3 3 1
—are the coefficients of (a + b)3; and so on.
To construct the triangle, write 1, and below it write 1 1. Begin and end each successive row with 1. To construct the intervening numbers, add the two numbers immediately above.
Thus to construct the third row, begin it with 1, then add the two numbers immediately above: 1 + 1. Write 2. Finish the row with 1.
To construct the next row, begin it with 1, and add the two numbers immediately above: 1 + 2. Write 3. Again, add the two numbers immediately above: 2 + 1 = 3. Finish the row with 1.
Example 7. Expand (x − 1)6.
Solution. According to Pascal's triangle, the coefficients are
1 6 15 20 15 6 1.
In the binomial, x is "a", and −1 is "b". The signs will alternate:
| (x − 1)6 | = | x6 − 6x5· 1 + 15x4· 12 − 20x3· 13 + 15x2· 14 − 6x· 15 + 16 |
| = | x6 − 6x5 + 15x4 − 20x3 + 15x2 − 6x + 1. | |
Example 8. Expand (x + 2)3.
Solution. The coefficients are 1 3 3 1. x is "a", and 2 is "b".
| (x + 2)3 | = | x3 + 3x2· 2 + 3x· 22 + 23 |
| = | x3 + 6x2 + 12x + 8 | |
Problem 9. Use Pascal's triangle to expand the following.
a) (a + b)3 = a3 + 3a2b + 3ab2 + b3
b) (a − b)3 = a3 − 3a2b + 3ab2 − b3
c) (x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4
d) (x − y)4 = x4 − 4x3y + 6x2y2 − 4xy3 + y4
e) (x − 1)5 = x5 − 5x4 + 10x3 − 10x2 + 5x − 1
f) (x + 2)5 = x5 + 10x4 + 40x3 + 80x2 + 80x + 32
g) (2x − 1)3 = 8x3 − 12x2 + 6x − 1
h) (1 − xy)7
= 1 − 7xy + 21x2y2 − 35x3y3 + 35x4y4 − 21x5y5 + 7x6y6 − x7y7
In the following Topic we will explain why the binomial coefficients are the combinatorial numbers. That will constitute a proof of the binomial theorem.
Next Topic: Multiplication of sums
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2021 Lawrence Spector
Questions or comments?
E-mail: teacher@themathpage.com
